We tend to approach decision-making as an exercise of an individual without taking into account that in many cases, our decisions are impacted by others. How do we approach that idea in decision process theory (Thomas, 2013)? One thought is to consider that decisions are based on the value or utility we ascribe to options (choices). Where does that value come from? Value for an option may be given or it can be created; value is often the fundamental driving force for a company.
A second thought is that value can be transferred from one person to another. There are several ways that can happen. In the theory of games, this transfer is “active” and a competitive exchange in the sense that what one person gains another person loses. What we have in mind here however is more along the lines of value creation than along the lines of competitive exchange. Cooperation between two or more people can result in the creation of value but still can be thought of as the exchange of value between members of the group. Though similar to competition, it is stationary; it does not change in time and is not dependent on active variables. This distinction is hidden in static theories of games. Value creation or cooperative value exchange results in a tidal bond associated either with the individual (individual value creation) or with pairs of members of the group (exchange of value from one to the other).
This concept of bonding arises naturally in decision process theory and leads to gradient forces associated with player worldviews, codes of conduct and even with time. Gradient forces have quite different characteristics from the competitive exchange forces that in form resemble Coriolis forces, which are velocity dependent along the active dimensions. What unites these three gradient forces is the concept of symmetries associated with inactive space or time directions.
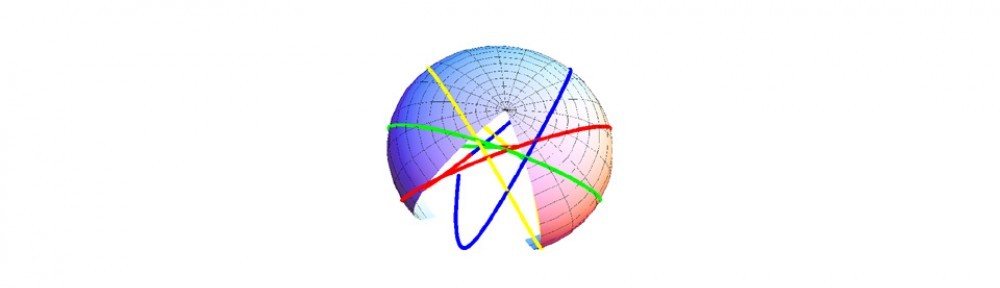
These concepts are essentially geometric in nature and can be illustrated with a familiar example of a rotating sphere such as the earth. The centripetal acceleration is a gradient force on any person or object standing on the earth, which tends to push that person away from the center of the earth. In contrast, the Coriolis force is zero if the person or object is not moving; if they are moving, then the force is along a direction orthogonal to the motion and dependent on the direction and magnitude of the earth’s spin.
A second gradient force is gravity which pulls the person toward the center. We must go into the depths of Einstein’s theory however to see that the gravitational force is itself a force based on a time symmetry. For our purposes here, we note only that in any dynamic geometric theory the two possibilities occur: one for time and one for spatial symmetries. We require somewhat more mathematics to describe mixing between space and time symmetries (Thomas, 2013). Leaving aside these subtleties, we can explore the consequences of the basic ideas.
What might we expect for bonding in decision process theory? For gravity, we have a gravitational potential that is static (independent of time), so we might expect a bonding potential 
What sorts of things can we infer from these observations? The total value creation 
These thoughts are translations of the theory; it is possible to examine the equations to verify that these translations are reasonable. Since this is only a theory, you might reasonably question whether these ideas apply in the real world. I think the answer is yes. In business parlance for example, value creation is an essential aspect of any decision process. Value creation can be something emotional as creating fear or joy. It may mean suggesting consequences that are unrelated to any payoff: for example, difficulty of execution, of getting paid, etc. It may in fact raise the value of the payoff in the sense of what is at stake, such as a new technological discovery.
Cooperative bonding is working together to create value for the organization. There is no sense of competitive exchange in either value creation or cooperative bonding as used in a normal business relationship. There is a cooperative exchange that is internal to the organization, which results in the transfer of value from one member of the group to another. Thus the concepts here we argue are in fact quite distinct from game theory payoffs, even though they also involve value.
In discussing value creation, value exchange and the new distinction of bonding (tidal bonds), we should also ask how these ideas relate to the notion of engagement. In decision process theory, engagement is a measure of the flow of choices, specifically the flow along one of the inactive directions. Its value fixes how often we do something or prefer something as opposed to how much value is associated with that choice. The potential confusion is that the payoff force may be the product of this coupling and the amount exchanged: this is the case for example in decision process theory.
The distinction between engagement and bonding is helpful. In building value, it may be very useful to not be engaged. In this area, such a person’s actions would appear entitled. The tidal bond could then be very large or very small; it is independent of the engagement. A consequence might be that in a neighboring area, the engagement would necessarily grow. The difficulty in describing these possibilities is the difficulty of keeping track of all of the related changes that can or should occur based on our understanding of how decisions should work. The advantage of a detailed and consistent theory is it makes such a description prescriptive and subject to well understood computational methods.
Given these distinctions, are there ways in which we act that encourage more engagement and different ways that encourage bonding? Engagement for example is how strongly we pay attention to reality, to what others are doing and thus to the consequences. It seems to me that this does not depend very strongly on how much value has been created or is being exchanged. To increase the value of what is being created or exchanged requires a different skill set. First we have to decide whether we are improving the value that we create or we are increasing some shared value. In the latter case, we are creating a code of conduct; our shared actions work in concert as if they were a single individual. The difference is that shared actions have to be agreed upon.
So to create something of value we first deal with an individual. What immediately comes to mind are individuals, who create something that is brand new: it might be an invention, a work of art or a work of science. It is not uncommon that during the creative act, such individuals are not particularly engaged in the world around them. If we are talking about a code of conduct, then in addition to creating something of value, we require all of the individuals to subscribe to a shared set of actions that support that code: this might be called a set of ethical behaviors or a corporate culture. This requires a new skill set, usually requiring some type of rote education in the sense that the code is not subject to debate.
The point of this education is not to make others be like us but to ensure their internal payoffs are robust and ethical (the common us) and reflect our shared code of conduct. What are the effective ways to teach? I shall call them “boil and freeze”. First it is necessary as in boiling, to make all states a possibility. For children this comes about naturally as one assumes that children provide a blank slate. Next one wants to create a new symmetry (a crystal form if you like) that reflects the desired code of conduct. I think we are familiar with this process even though in its extreme form it may cause great harm. For example a war is a type of boiling, as is a cultural revolution. In businesses, there are less extreme forms such as reorganizations and forms that follow the dictum “if it ain’t broke, break it!”
To create the desired symmetry or code of conduct there are many well-known approaches. Provide a mentor or role model and require all the students to adopt that mentor’s behaviors. Provide students with many problem solving situations and allow them to come to the conclusion that a particular code of conduct is the obvious solution. For these methods to work, the student must be engaged.
Students may learn through experience only if they are strongly coupled to what happens. Their ability to engage is a mental muscle. Another mental muscle is their ability to cooperate. In this case it is not engagement but bonding. Cooperation requires pairs of people to form a bond. So students must create bonds with others: other students and with their teachers or mentors. Such bonds induce sharing and an exchange of values. There are many examples in the market place of these types of activities. To name a few examples, consider advertising and sales as attempts at creating bonds and enrollment as a way of identifying where bonds may already exist.
The other aspect of bonding is cooperative exchange. What mental muscles are required? It is again related to learning, though not necessarily the rote learning style required to adapt people to a code of conduct. This type of learning is more interactive since it means identifying something of value that someone else has, being critical of what you learn so that in fact you may create more value and may cause the teacher to be the student. This type of learning is a two-way exchange as opposed to rote learning.
The take away is that realistic decision-making requires new distinctions of bonding as well as engagement. Such distinctions are clearly a part of the normal discussion in the real market place and so must be part of any realistic theory. We don’t claim to have the only theory that has incorporated such ideas, but note that the way in which we have done the incorporation is self-consistent and provides the ability to compute the numerical behaviors of these attributes over time.
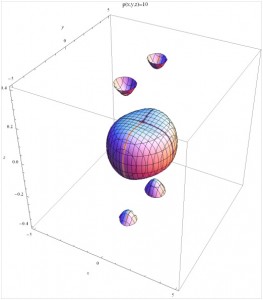
So we can look at the numerical behavior of two quite different concepts. One is the concept of energy density or its equivalent pressure, that essentially act like the potentials associated with the time symmetry of the fixed frame model.
The picture is particularly nice since it makes the analogy with the earth even more explicit, while also showing that there can be interesting differences. The shape is not quite a sphere, for the particular model assumptions used. There are some indications of additional structures. The fixed frame model used here describes an attack-defense model (Thomas, 2013, p. chapter 8) in which each player can choose between two strategies. We choose one code of conduct strategy which generalizes the game theory notion of a zero-sum game. Though code of conduct makes the choice sound noble, it may not be as in this example of a war game. This leaves three active strategies: one attack strategy (“first player”), one defense strategy (“second player”) and one strategy that measures the intensity of each player (the difference of the sums of each of their strategies, here plotted in the vertical direction). See the reference for details. It is not true, but approximately true that the normal to the surface gives the gradient force associated with the time symmetry (gravity).
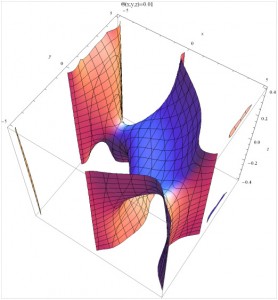
The next picture provides the total value creation in the same model. This provides a first view of how the overall tidal bonds reflect the energy density (pressure) distribution. The reference provides detailed information on how the various theoretical parameters are related to these pictures, which summarize the conceptual distinctions that are new. The pictures show how we envision making these distinctions quantitatively useful. Just as gravity as an idea becomes more useful when we associate a force with the concept using the notion of the gravitational potential, we gain more than just qualitative insight by identifying the bonding potentials and their associated forces.