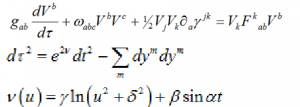Introduction

This talk continues an inquiry into the relationships between decision making, determinism and chaos: an initial in-depth exposition can be found on this site. Decision making is one of the most human acts and seems to be the most difficult area to formalize into a theory of behaviors that are causal and deterministic. In fact one might think that the very nature of decision making is one of chance and uncertainty. One issue we think relevant is a lack of appreciation on how causal theories deal with uncertainty. In the view of many, there is insufficient understanding of the sensitivity of the dynamic behavior on the initial conditions. When these issues are taken into account, it becomes easier to see the possibility for causal formal theories of human decision making. See a related and much earlier MIT paper on this subject based on Systems Dynamics, Sterman et al.

One thing that might help our understanding of these issues is to explore how we deal with uncertainty in such mundane activities as measurements, which form the basis of physical theories. So for example, we understand by length, an attribute that characterizes the height, width or depth of something. It is a great accomplishment in understanding to separate this concept from the mechanisms by which we perform the measurement. The mechanisms involve a measuring stick and us as agent; for those of you measuring a basement, you know that multiple measurements yield multiple answers. Yet we are confident that the basement has well defined dimensions. How did we come to this conclusion and how did we learn to separate out the uncertainties associated with us as agent and the intermediary of a measurement stick, from the invariant concept of length? I think we all agree that the separation has been done and we are comfortable with the idea of length.

This distinction in measurements can also be made when making decisions. There are aspects of decisions that are uncertain which mask potential underlying relationships that are causal. As an example I may choose between several strategies according to a fixed set of frequencies that behave according to a deterministic causal theory, yet there can still be an uncertainty in measuring the exact numerical values of these frequencies. More importantly I may not know what choice I will make at some future time even though the frequency of choices is known. There is no requirement that a causal theory of decisions needs to address that issue. Indeed to construct a causal and deterministic theory we may be better off not including such uncertainties in our theory, just as in physics we are better off not including the measurement process. Such processes are usually treated as stochastic with no dynamic structures.

We distinguish such measurement uncertainties from the dynamic uncertainties that result from sensitivity to initial conditions. The latter lead to chaos, showing that deterministic causal theories can have rich dynamic structures with understandable regularities, in contrast to stochastic behaviors. To present these important concepts we proceed as follows:

1. introduction
2. decision making
3. determinism and chaos
4. elasticity
5. determinism and chaos in decision theory
6. fixed frame models–complete solutions
7. conclusions

Decision Making

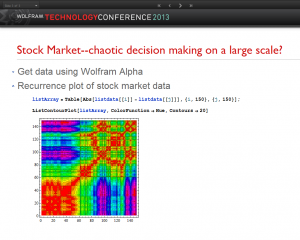
We note that many decision making behaviors that appear to be uncertain may well have causal elements. For example the behavior of the stock market, which is clearly an example of decision making, appears often to have elements that are uncertain. However if we observe the time series behaviors of the stock market using recurrence plots, we see causal systematics:

Here we have captured the behavior of a particular stock using Wolfram Alpha and created its recurrence plot. The details can be found in the CDF file, which allows the reader to further explore such plots using different stocks.

Determinism and Chaos

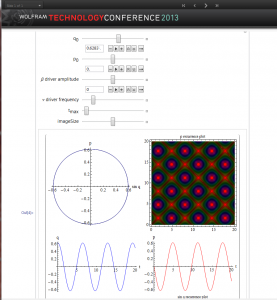
The other extreme of uncertainty would be to consider behaviors in the physical world which are assumed to follow well understood laws. A simple example can be taken from physics and the motion of a pendulum. Here non-linear spatial behaviors can also manifest as non-linear time behaviors, including behaviors called chaotic.

Without making a small angle approximation, for low amplitudes the behavior is periodic. There is no structure. However, the force on the pendulum is not proportional to the angle but to the projection of the force along the vertical direction. This introduces a non-linearity. The consequence can be highlighted in a number of ways. One is to provide a oscillating harmonic force on the pendulum. Alternatively, one can start the pendulum with an initial but large velocity. Here is a typical result.

The CDF file allows the reader to experiment with different initial conditions and different values for an external harmonic force. One of the consequences of this deterministic behavior is chaotic behavior. By this we mean that the behavior depends sensitively on the initial conditions. Even though the equations are causal the resultant behavior appears uncertain; in reality the uncertainty is an artifact of the initial conditions, not of an underlying uncertainty in the physical process. The underlying dynamics impose regularities on such chaotic behaviors that have been extensively studied. There is an inter-play between what happens in space and what happens in time.  We believe such interactions also occur in decision making.

Elasticity

We believe that decisions have not only a causal connectivity but a strategic connectivity. We adopt conceptual game theory that decisions are characterized by players or agents that each decide from a list of pure decisions, assigning a frequency of choice to each. From a mathematical perspective each game is decided by these frequencies which represent a point in this space of strategies, spanned by all possible frequency choices. we focus on games which are played multiple times so that we observe both the time evolution and the spatial connectivity. The hypothesis is that decisions change continuously in time and strategy space. We call connectivity in time causal. We call connectivity in strategic space elastic. Spatial elasticity may be related to network connectivity, whose importance is argued by Barabasi.

Game theory, as opposed to our restricted version of conceptual game theory, usually deals with an equilibrium situation, so the idea of causality and elasticity are outside of the scope of the theory. They enter indirectly in the problem statement. We make arguments about the payoffs, which are the key elements of the theory that lead to a specification of the strategic frequencies at equilibrium. what we ordinarily don’t do is assume that the payoffs can change over time. We also don’t consider the possibility that the payoffs and the frequencies are not simply tied by an equilibrium condition.

To explore how this works, we can take any game and see how various decision attributes such as payoffs and frequencies might change over time. We can use the sliders in the CDF model to simulate time. As an example we take the children’s game of rock, paper scissors.

In practical terms, a way to do better in the game is know something about your opponent. If they don’t like playing certain strategies, you are better off adjusting the payoffs to reflect that. As they learn about your behavior, they adjust their behavior causing you to readjust your behavior. You can experiment with the above model to see the effects. In this picture, we assume that the payoffs are in fact given by their equilibrium values. Shortly we remove that restriction.

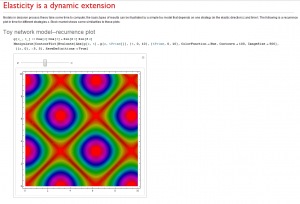
What we learn from this is that there are degrees of freedom that can change independent of time. We call it space as an abuse of language: we mean strategic space, not physical space. We anticipate that changes in space will influence changes in time. A simple model to illustrate a network model with elasticity is the following:

If you change the spatial variable, the time recurrence pattern changes. It illustrates what we see in the general theory without the corresponding mathematical complexity. The key concept we propose is that decisions are causal and elastic: they depend jointly on time and space variables. Because of the interconnectivity, the resultant behavior is analogous to an elastic medium, which can exhibit waves that propagate, reflect and possibly die out. This goes beyond game theory as well as simple Systems Dynamic models. We now make these ideas more precise.

Determinism and Chaos in Decision Process Theory

Just as in physical models, we have a causal dynamic model in mind. We take these ideas from decision process theory and the behavior along a streamline:

We start with a set of equations:

The first equation sets the rate of change of the frequencies that determine strategic choice. On the left is the rate of change of those changes and on the right is the effect on those changes based on the payoffs. When the payoffs are zero, the rate of change on the left is zero. We consider more general changes here. The second and third equations determine the response of the equations to harmonic forces, analogous to those for the pendulum.

Time dependence occurs in the above equations even if the payoffs are independent of time. We see that the frequencies no longer are constants but may oscillate and exhibit other dynamic behaviors just because we are no longer at equilibrium. Shortly we will also consider the possibility that the payoffs also vary in time. But for now assume that they are constant.

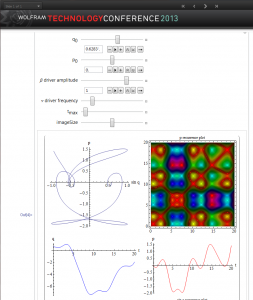
We consider a prisoner’s dilemma model in which we can change the various parameters that govern the payoffs. In addition we can change the relative weights of the payoffs for each player, which can introduce non-linear effects independent of the harmonic forces.

When we have small oscillations away from equilibrium, as with the pendulum we see harmonic behaviors for all of the strategies as seen above.

However as we either add more harmonic forces or move away from small oscillations, non-linear behaviors result as shown above. We get chaotic behavior for some choices of the parameters. One can play with the details using the CDF model.

Fixed Frame Models–Complete Solutions

The other source of causal and elastic behavior occurs when the payoffs can also vary. Decision process theory provides for that possibility. There is a soluble model (numerically); the one we choose is an attack-defense model. With a suitable choice of parameters, we again observe non-linear behaviors:

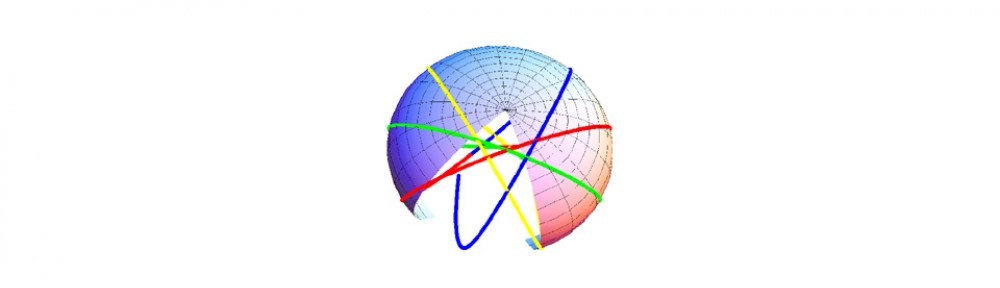
In these figures, there are four possible strategies in an attack-defense war game in which one side defends two targets (one high value one low value) and the other side can attack the two targets. The standard game sets payoffs for the four cases. We no longer assume here that the game is played at equilibrium. We assume only that the sum of strategies (actually preferences in the theory) is conserved, leaving three strategies that can vary. Along a streamline, we view the behaviors of the payoffs as functions of time and three parameters that characterize the strategies along the streamline: x, y and z in the figure. Using sliders we can see how the phase space plot changes. This model is somewhat more complicated and is too large to provide in this talk. So in this case we just provide a couple of illustrative examples.

We see the same type of qualitative behavior as before, without making any assumptions about the form of the harmonic force; it is an outcome of the theory in this case.

Conclusions

In general, chaotic effects require non-linear behaviors. We have observed such behaviors in a decision process theory and expect to see such behaviors in realistic decision processes, including stock market behaviors. These behaviors depend on both causal and elastic effects. The new ingredient is paying attention to the elastic components of decisions: both payoffs and frequencies can vary in time and strategic position.