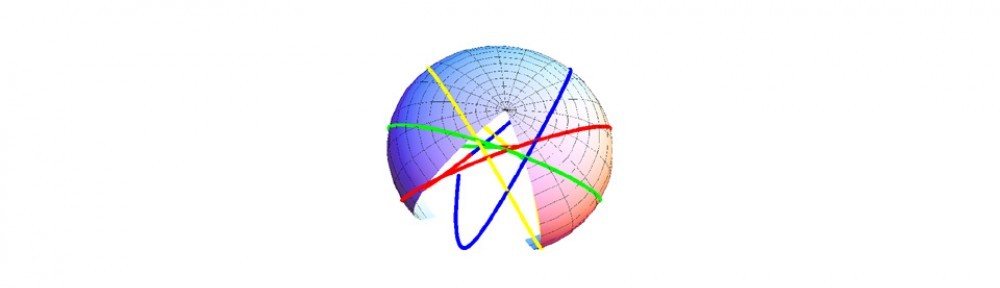
A key to understanding dynamics is evaluating the shortest path between two points. A realistic and modern understanding of dynamics consists of looking at the shortest distance between points embedded on a curved surface. A very nice conceptual way of thinking about such questions is in fact quite old and consists of looking at the distance of two points on a sphere. This can be extended to considering not just a sphere but an oblate spheroid, the actual geometry of the earth.

It is found that the geodesics on an oblate spheroid are much more complicated than the great circles on a sphere. The following geodesic was computed using Mathematica. A detailed description of the method and a Mathematica CDF notebook is provided. The figure of a single geodesic became the logo of my first book on decision theory, Geometry, Language and Strategy, Thomas, 2006, World Scientific (New York). The figure is reproduced below and can be rotated using the mouse pad once you have installed the free CDF Reader.

[WolframCDF source=”http://decisionprocesstheory.com/wp-content/uploads/2012/08/logo.cdf” width=”580″ height=”720″ altimage=”http://decisionprocesstheory.com/wp-content/uploads/2012/08/logo.cdf”]