A classic game theory model for a tyrant might be a game of chicken, with a tyrant against the poor, each choosing between swerving or crashing. The difference however is that a tyrant has more power and influence than the poor. One aspect of game theory that we believe needs to be changed is that the size of the payoffs should matter.
As an example of something that plays no role in game theory, consider the concept of engagement. Multiplying the payoff matrix by the engagement does not change the max-min solution of game theory and is thus of no importance. Moreover, the payoff matrix strength is not relevant either. In physics, this is like saying that the charge of a particle does not influence its motion in a magnetic field, nor does the strength of the magnetic field. This is only true for a charge moving parallel to the field. The circulation around the field clearly depends on the charge as well as on the strength of the field.
The hard part is to disentangle the charge from the field strength. This is accomplished in physics by the field equations that say that charges and currents are the sources of the fields. Strong engagement leads to changes in the players behaviors through changes in their payoff and valuation fields. What is amazing however, is that engagement like viscosity enters the decision process theory equations in a non-linear way. Therefore, dramatically increasing or decreasing the engagement changes the qualitative behavior of the decision flow. You get an inkling of why when you realize that the engagement is itself a conserved flow and therefore contributes to the energy momentum of the system. It thus gets shared with other component parts.
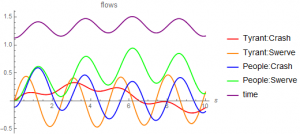
Like viscosity, when the engagement is small it has almost no effect other than adjusting the time scale. As it gets larger, the non-linear nature of its behavior becomes evident. It is even possible that we might get “chaotic” or “turbulent” behaviors, though there is currently no basis for this conjecture. The following is the result of a computation (using a decision engineering notebook described in the Stationary Ownership Model Update white paper and implemented using a Mathematica notebook) in which the poor outnumber the tyrant by 10:1 and the engagement of the tyrant to the poor is 1:10.
We have the following interpretation of this picture. From a game theory perspective, the model has two Nash equilibriums. The poor see their strategy to be “swerve” and assume that the wealthy will “crash”. The wealthy see the opposite. This is one variant of the classic game of chicken. It is clear in the figure that by assuming the wealthy are much less engaged, we are closer to one of the Nash equilibrium: we see the Nash equilibrium of the poor, which is to “swerve” and for the wealthy to “crash”.
We see more however. Because of the inequality between the two players, the preference of the poor to crash is going to be smaller over time than for the wealthy to crash. So, in some sense, the wealthy crashing is not as devastating as it is for the poor. There is much less incentive for the wealthy to avoid the choice “swerve”.
The strategic flows add some interesting aspects to the story. The magnitude of the flows in this model run are all comparable. Nevertheless, they support the fact that the net behavior for the wealthy to swerve is zero and the net behavior of the wealthy to crash is small and positive. It is also clear that the net flow for the poor to swerve is much bigger than any of the other net flows.
We interpret this as follows. The poor will suffer and avoid the game of chicken. On average they will swerve. The wealthy will crash, making what appears to be the correct assumption that the poor will always swerve. These assumptions, however, rely on the small engagement of the wealthy. This appears to be the trademark of the tyrant They suffer no consequence for their action and are thus rewarded. The full decision process theory would go on to predict that the payoffs for the wealthy should not change since their source is small. The poor however might change their payoffs over time to better reflect what is happening.
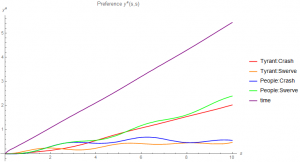
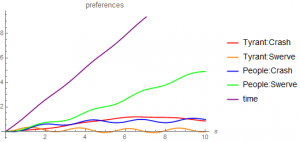
Is there anything that can be done? One possibility is demand an equality of effort between the tyrant and the people, through laws, the courts or the press, as examples. An example computation is provided below, using a gravitational like field to force equality by imagining a potential well that is centered when the strategic effort of the poor matches the strategic effort of the tyrant.
The model generates a time component of the metric, which can be thought of as a “gravitational” field that pulls all strategies to this common center. We see the consequence of this in the above figure. We now expect that the tyrant will see consequences to their action, despite their initial lack of engagement. In fact it might be that that engagement will also change as a consequence.