It seems to me that inequities start from the following type of conversation. There is a misperception among people I talk to that I actually wish to contribute to their capital in some way; that they have some enormously interesting endeavor, which I am dying to become a part of. If I contribute in this way their capital grows. There is no reason to suppose that my capital grows as an outgrowth of this exchange. If one person is wildly successful in getting people to contribute to their capital, they will amass a large fortune at the expense of many contributors, each of which lose little perhaps, but also each gains little.
This phenomenon may be related to the ideas in a new book on capital that speaks about the growing inequality of capital (Piketty, 2014), though capital is now used in its proper sense. From a theoretical viewpoint, I think this is related to decision process theory. In that theory, substances tend to accrete into big piles. When these piles become sufficiently large, they may create stable structures. I have not shown that to be the case, but such behaviors occur in physical theories that are similar. If it did occur, we would have a dynamically created code of conduct.
The idea of capitalism, as expressed by some, is that all boats rise together so there is an advantage to rewarding the entrepreneur. The argument against, by others, is that vast inequalities may arise in which one class does not rise at all. Such class members get submerged, to continue the metaphor. A theory should be able to demonstrate both behaviors and give the necessary and sufficient conditions for each behavior to be stable. In the theoretical view, for the first argument, each individual’s payoffs or desires cease to be important; only the payoffs of the dominant player are important. In this way their desires are not satisfied. At some point they must complain. As individuals this may not be sufficient to change the new status quo. Hence they must unite in order to make an impact.
This outcome need not be the only one since a modest redistribution of effort might honor the payoffs of most people while cutting back only slightly the capital going to the dominant player. Alternatively, there may be a world in which there is no dominant player, only a dominant strategy, one that everyone individually desires. I think that that strategy can’t be becoming wealthy (in terms of money) since that means most people will become poor, in terms of money. Of course the theory does not require that outcomes be measured in terms of money, only in terms of things that are valued by the player.
Nevertheless, suppose we buy into the concept that we should act based on our self-interest. This is supported perhaps by the theoretical view that we act based on our internal view of the payoffs. I say perhaps because it is not a given that our internal view of payoffs totally reflects our self-interest. To act purely in our self-interest against others who also purely act in their self-interest suggests a great deal of effort needed on our part to defend ourselves from attack. If we could agree with our fellow antagonists on some ground rules for such fights, we might be able to reduce the time we spend on defense and increase the time we spend gaining those goals we really strive for. Such an agreement on ground rules changes the nature of the interactions by adding a code of conduct. We need to be regulated. The best regulation is one that is minimal; it is best from the standpoint of where we start from, which is as antagonists.
Of course we might start from another position of being communal, in which case we might have somewhat more regulations. However there would be I think a need to limit the regulations so as not to totally smother the members of the community.
This line of thought suggests a zero sum or constant sum code of conduct. If we give something of value we should get something in return of comparable value. This “regulation” prevents outright theft and banditry. If nobody feels they are being taken advantage of, they need not spend their time defending their possessions. I suggest this might be the basis for monetary systems. I note that such regulations necessarily reflect conserved quantities in the theory. Perhaps there are reasons why such conserved quantities come into existence and form relatively stable structures. For the moment, let us just say that we have provided plausible reasons why they might exist.
So how do we proceed? I think we have to imagine what the code of conduct would be in a variety of stable configurations. Each configuration might have several components. To start, I suggest making the distinction of fair exchange between two players  : this occurs when their distance scales
: this occurs when their distance scales  is inactive. A related distinction is when the strategies
is inactive. A related distinction is when the strategies  form a coalition: this occurs when their sum is inactive. I think this can be generalized in a nice way to mean that these strategies form a surface. A special case is the constant sum game: the coalition consists of all players and their strategies. Although rather simple, I think these two distinctions revise both chapters 6 and the beginning of chapter 8. There is I think a new taxonomy to be considered. It includes the cases currently done but does suggest new possibilities, such as four strategies all part of a single player.
form a coalition: this occurs when their sum is inactive. I think this can be generalized in a nice way to mean that these strategies form a surface. A special case is the constant sum game: the coalition consists of all players and their strategies. Although rather simple, I think these two distinctions revise both chapters 6 and the beginning of chapter 8. There is I think a new taxonomy to be considered. It includes the cases currently done but does suggest new possibilities, such as four strategies all part of a single player.
In suggesting revisions, I have in mind keeping the distinction of the internal (hidden) nature of the players. Their nature is hidden in the sense of hidden variables and constraints that I don’t wish to explicitly take into account. These hidden variables are private and inactive. They result from processes that are not publicly shared and take no direct part in the strategic decision processes. As with constraints in physical processes, we don’t need the details of these processes, just their effect in the energy considerations.
I also keep the notion that there are active variables, which all players agree are part of the decision making process. It may happen that some of these variables or collections of these variables are part of a code of conduct, which could mean there is a coalition. A coalition acts just like an inactive variable in all respects, except that these inactive variables are public; all players are aware of these degrees of freedom and so they form a necessary part of the solution to any decision problem. To make the distinction clear, when there is a doubt, I now call such variables code-inactive. I include the fair exchange and possibly other distinctions as they become known in this set as well. I will call the hidden inactive variables private-inactive.
Another possibility for a code-inactive variable is time. Time is interesting since we normally don’t think of time as a strategy. Yet I have considered time as the hedge player that allows a symmetrized version of the game. It thus has structural significance. As a stretch distinction, it is the learning strategy which brings us into the future. From this formulation, it is clear that time and space strategies are being treated on the same footing, with the exception of the metrical difference with time. Thus for time to be a code-inactive variable, I suggest that learning is occurring at a steady (conserved) rate. The code of conduct thus may consist of different types of code-inactive variables: the learning strategy; coalitions; and fair exchange.
For every inactive variable, there will be a payoff matrix. This is true whether or not the variable is private-inactive or code-inactive. For any solution of the active variable problem, there will be a reduction to an equivalent problem that includes code-inactive variables. This problem will have payoffs for the expanded set of players that includes the code of conduct. Once solved, one can go back to the original problem and compute the payoff matrices for each of the private-inactive players. These are the native players that provide the definition of the private-inactive variables. This has been the approach of the numerical computations carried out so far.
What provides new insight is that these different types of codes of conduct, in different combinations, lead to different solutions; we have expanded the taxonomy of possible behaviors. We have to understand in more detail what decision process we have in mind. For example, the notion of a game is centered on the idea of their being payoffs. Whenever we have payoffs we essentially have a game. For any game we should look for the code of conduct which defines the game; it is the strategy that is orthogonal to all the strategies that are active in the exchange.
We say more by characterizing the types of forces that must be associated with a code of conduct. We take this from the theory. First and foremost is the exchange or payoffs that reflect a competitive push-pull force made famous in game theory. It has analogs in physical theories: Coriolis forces in mechanics, magnetic forces in electromagnetism. The second force is less well known in economics, but we believe is also important: a gradient force whose behavior is set by surfaces of constant potential and whose strength and direction are set by the gradient normal to that surface. When the learning strategy is part of the code of conduct, we expect and see in our computations a gradient force that encourages an accumulation of value, of wealth. Other codes of conduct produce forces that discourage such accumulation. In physical theories, gravity and centripetal forces provide examples respectively. We suggest looking for such forces for each code of conduct.
You might consider it natural that the overall decision is characterized by a coalition of the whole: it is a constant sum game. From this we expect payoffs or exchanges. Indeed it is also natural to consider that economic behaviors in general are characterized by the exchange of money and value. Moreover, economic behaviors are also considered to involve fair exchange. We see a strong reason for agreeing with (Von Neumann & Morgenstern, 1944) that such behaviors should be considered as constant sum and fair exchange games with a learning strategy. This however does not mean every application of decision process theory should be thought of as such; only a subset of applications with this particular set of codes of conduct.
For example, we can have a Robinson Crusoe environment in which the total scale is not constant. This works not only for a single strategy controlled by one person, but for multiple strategies controlled by a single person. Clearly this can be generalized to multiple players where the overall sum is not a constant. These are not constant sum games. We might envision that of such possibilities, there will be those with a fair exchange between every pair of players, which thus identifies a different code of conduct. This is not the game theory of (Von Neumann & Morgenstern, 1944). Yet it is an interesting model that we can study in detail. A particular example to revisit might be the prisoner’s dilemma.
We are now ready to return to the question of inequalities in economic behaviors. Why might one group get rich and another group get poor? In our formulation of game theory, we consider not only games that are constant sum, but games in which there is fair exchange between each of the players including the learning strategy. Thus each player scale is part of the code of conduct. If we relax the idea of fair exchanges and even perhaps the idea that the learning strategy are inactive, then our results may generate inequalities and thus shed light on how inequalities would occur as a consequence of the theoretical assumptions. We might learn whether such behaviors are stable or not. To date, we have not focused on behaviors associated with inequality in our numerical computations. This is something that should be done.
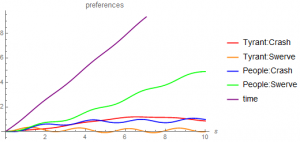 We have the following interpretation of this picture. From a game theory perspective, the model has two Nash equilibriums. The poor see their strategy to be “swerve” and assume that the wealthy will “crash”. The wealthy see the opposite. This is one variant of the classic game of chicken. It is clear in the figure that by assuming the wealthy are much less engaged, we are closer to one of the Nash equilibrium: we see the Nash equilibrium of the poor, which is to “swerve” and for the wealthy to “crash”.
We have the following interpretation of this picture. From a game theory perspective, the model has two Nash equilibriums. The poor see their strategy to be “swerve” and assume that the wealthy will “crash”. The wealthy see the opposite. This is one variant of the classic game of chicken. It is clear in the figure that by assuming the wealthy are much less engaged, we are closer to one of the Nash equilibrium: we see the Nash equilibrium of the poor, which is to “swerve” and for the wealthy to “crash”.