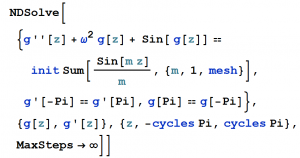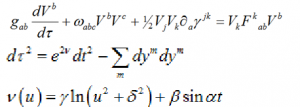Are there resonant circuits in General Relativity?

Posted on January 19, 2015 by Jerry

For some time I have been exploring behaviors in differential geometries, one of which is the geometry of General Relativity. I have also been looking at circuits in electrical engineering and was taken with the idea of resonances. They occur in circuits that have an inductor, capacitor and a resistance. Resonances also occur in physical media such as musical instruments, bells and bridges. In all of these cases, one can “drive” the system with an oscillating force and observe the possibility of resonance by the appearance of a super strong response to what may seem like a small driving force.

Alternatively, one can look at such systems without a driving force and start it from some initial condition; one then observes the system “ringing” or resonating for some time thereafter.

We approach such systems ordinarily as being described by linear equations and think of the two cases as examples of solutions to such equations that have both homogeneous contributions (the latter “ringing” solutions) and inhomogeneous contributions from the driving force. For the inhomogeneous contributions, a wave solution at a given frequency results in a steady state solution of the same frequency with an amplitude determined by the details of the media. For the homogeneous contributions, there is no initial frequency, but typically an algebraic equation determines the resonant frequency possibilities; there are only a finite number of such solutions.

You might think the situation is different in the differential geometries that I have been considering. The equations are not linear. There is no longer the presumption that small changes in the initial conditions lead to small changes in the resultant behaviors. For example one might get “chaotic” solutions from the simplest of forms.

However, I think one can still analyze such systems in differential geometry as if they were resonant systems. The basic idea is that resonance effects should manifest whenever the various energy contributions cancel in the sense that they leave a system that looks like there are no external forces. I can put this thought into the equations for a differential geometry theory.

${{g}_{ab}}\frac{d{{V}^{b}}}{dt}={{f}_{ab}}{{V}^{b}}+{{T}_{a}}$

The left hand side is the acceleration in the theory, which depends in part on the metric field. In general the theories have isometries, symmetries that leave the metric unchanged, and these isometries lead to “electromagnetic fields” or Coriolis Forces. The first term on the right represents such a contribution. Finally there will be a host of other effects, which reflect various contributions that drive the curvature of space-time, such as inertial stresses. We think of these terms as forces that “drive” the behavior. They are the analog of forces in a circuit. If we take the analogy seriously, we speculate that resonance occurs when these forces cancel: ${{{T}_{a}}=0}$ .

What I find interesting is that the equation that remains is a homogenous equation that has discrete solutions if the assumed flow is harmonic:

${{V}^{a}}={{\tilde{V}}^{a}}{{e}^{i\omega t}}$

The reason is that the resultant equation is an eigenvalue equation for the frequency:

${{f}_{ab}}{{\tilde{V}}^{b}}=i\omega {{g}_{ab}}{{\tilde{V}}^{b}}$

The possible frequencies are based on the eigenvalues of an antisymmetric matrix ${{f}_{ab}}$ ; the eigenvalues are zero or purely imaginary. Thus the solutions lead to a discrete set of real frequencies. I suggest that these are the resonant frequencies of the “circuit”.

There are a variety of interpretations, depending on the details of the differential geometry. For example, for general relativity, the antisymmetric matrix could be the Coriolis force and reflect a rotational frame. It could also reflect the electromagnetic field and the rotational field is the magnetic field. For decision process theory, the matrix can represent the payoff field. In each of these cases, one expects that there will be essentially a “free fall” solution that has a discrete set of frequency contributions. In addition, there will be solutions with any frequency, but such solutions will no longer be “free fall”. They will correspond to having a non-zero “driving force”. It is interesting that we find both types of solutions in the numerical exercises for decision process theory.

It is interesting to speculate on whether there are physical manifestations of such discrete solutions in physical processes such as transmission lines. I think the usual analysis does not indicate the possibility. The possibility might occur however if one considers transmission lines in magnetic fields or possibly with additional symmetries, such as circular transmission lines that rotate.

WTC-2014: Visualizing behaviors in differential geometries using Mathematica

Posted on November 10, 2014 by Jerry

Introduction

This talk was given at the Wolfram Technology Conference in October 2014 at Champagne, Illinois. The idea of the talk was to explore how one visualizes behaviors in differential geometries that are more complex than the usual three-dimensional flat geometries we are familiar with.

Abstract

We use Mathematica to visualize such behaviors. Our access to these behaviors are the partial differential equations that describe the shape of the geometry; these equations provide us a way to track the shortest paths. Shortest path algorithms are familiar from Newtonian mechanics, geometrical optics, Maxwell’s theory of electromagnetism and Einstein’s theory of relativity. My particular interest has been the possibility of using the shortest path algorithms of differential geometry to solve problems in the social sciences; in particular to gain insight into the causal behavior of decision processes. In this case, the starting point is the conjecture that decisions are events that form a continuous manifold in both time (causality) and space (strategies). This is a fundamentally different starting point from the usual stochastic approaches used in the social sciences. The resultant behaviors are shortest paths in a differential geometry space.

The challenge is to visualize these behaviors that are consequences of the differential geometry. This talk addresses that challenge. We apply Mathematica solutions to the partial differential equations and look at limit cycles and limit surfaces and their relationship to harmonic solutions and chaotic behaviors. We proceed with model solutions using Mathematica of more complicated differential geometry possibilities that have applications to gravitational theories and decision theories. We find that the NDSolve and Manipulate functionality can be used to great advantage in order to visualize the behaviors in these geometries. There are many other applications of these visualizations, such as teaching possibilities in Electro-Magnetism courses.

Outline of talk

Decisions as Geometry
- Take an example www (work-wealth-wisdom) model
- What is time? What are space components? How is uncertainty dealt with?
- Idiosyncratic behavior and symmetry
Steady state solutions
- Can steady state be chaotic? Jupiter red spot!
- Examples from WWW–rotations, Coriolis, magnetic fields and payoffs
- Need to solve complex stationary problem
- Use harmonic series approximation
- Do we exclude chaotic behaviors? See toy model . Build on this with harmonic solutions
Decision geometry is more complicated than in physics
- Two different transformations to stationary frame–two versions of time flow
Communication travels at a finite speed
- There are communication ellipses

Decisions as Geometry

There are many examples of geometry in the physical world, starting with the most familiar, the geometry of the earth. Many theories, such as Newtonian mechanics use geometry in a variety of contexts that extend the notion of purely flat space to spaces with curvature. The most striking example is perhaps the theory of Einstein, which maintains that our “normal” space is 3+1 curved dimensions. The specific behaviors of geometry that we find interesting are:

Position and Uncertainty
The nature of time
Symmetries

These are particularly interesting to us because of the possibility of using geometry to describe how we make ordinary decisions in the business and economic world. We have presented these ideas at past Wolfram Technology Conferences; many more details can be found on my website.

Position and uncertainty: Let’s deal with position and uncertainty first. At least some of us think of position as described in physical laws as certain, and think of “soft” concepts such as decisions as inherently uncertain. That is perhaps not the full story. It is true that at least starting with Newtonian physics, the concept of position is considered as something that is well-defined and certain. However, the measurement of position is not. Anyone that has measured a room knows that every time you make the measurement you get a slightly different number. Thus the key insight in Newtonian mechanics is to separate the concept of position from measurement: the certain concept from the concept that has a degree of intrinsic uncertainty.

We suggest a similar type of split is necessary for considering decision making, a split that has been made in the Theory of Games. The concept of utility can be applied to preferences as a well-defined concept of certainty. However the measurement of preferences involves observing the frequency with which we make our choices. For any given decision point, we make one choice out of several, which is uncertain. Nevertheless our preferences, like position, might be considered as certain. As with game theory, we take as a point in space, the collective strategic preferences of each decision maker.

Time: Let’s deal with time next. In physical processes, we can think of time as Newtonian, meaning we ascribe an absolute time as being applicable to all events happening anywhere throughout the universe. Alternatively, we can think of time as Mawellian, meaning we ascribe a local time to the events happening in our vicinity, and potentially a different time for events happening elsewhere. It seems to be a less efficient way of talking about time, but does allow for the fundamental fact in Maxwell’s description of light that light travels at the same speed regardless of frame of reference. Einstein took up this argument and concluded that in this respect Newtonian mechanics needed to be modified to conform with Maxwell’s description.

As a rule, we describe physical processes as causal in nature. Once we agree on a definition of time, we incorporate that description into the way we see the world. Events happen in succession with earlier events having the possibility of influencing later events in a strict cause and effect relationship. Not all events have such a relationship. Statistical events may occur in such a way that later events are independent of all earlier events. A particular type of such an event is stochastic. Wikipedia says: “In probability theory, a purely stochastic system is one whose state is non-deterministic (i.e., “random”) so that the subsequent state of the system is determined probabilistically. Any system or process that must be analyzed using probability theory is stochastic at least in part.^[1]^[2] Stochastic systems and processes play a fundamental role in mathematical models of phenomena in many fields of science, engineering, and economics.”

What stance do we take? Do we assume a causal behavior or a stochastic behavior? The current literature favors the idea that decisions reflect stochastic processes. We take the opposite point of view: We follow the lead from those that have applied Systems Dynamics to a variety of real world problems and conclude that many real world problems can be treated as causal. Having taken this stance, the next question is whether we take a Newtonian view or a Maxwellian view. We have studied decisions starting from the formulations of the Theory of Games and note that the underlying concept of payoffs closely parallels the concept of magnetic fields and so adopt the Maxwellian point of view.

The key conclusions we make for our study of geometry of decisions is that it be based on positions as determined by strategic preferences and time as a local variable subject to the constraint that information move at a speed that is locally the same to every observer in the system. This is similar to the geometries envisioned by Einstein in his theory of general relativity. It is much broader however in that the number of dimensions is not limited, but depends on the number of pure strategies available to the collective of decision makers. The local nature of space and time so defined relies on the existence at each point of a set of potential fields, one for each dimension of space and time. A surface of constant potential is one on which we have a single well-defined value for the amount of distance or time is appropriate to that coordinate. We can call these coordinate surfaces. On a map of the earth, these would be the lines of constant latitude or constant longitude; these have a meaning on a flat chart despite the fact that the lines represent a spherical (or oblate spherical) earth. In higher dimensions these lines we call hyper-surfaces, or simply surfaces.

Symmetry and idiosyncratic behavior: Common physical systems often exhibit symmetries that are an essential part of how we think of them. The earth is symmetric about its axis; indeed it is almost spherically symmetric. Such symmetries are reflected in the way we describe the geometry. Let’s pursue as an example the axial symmetry of the earth. The oblate character is reflected in the behavior of the latitudes and the symmetry is reflected in the way we treat the longitude. There is no difference in the shape of the earth at different longitudes. Newtonian physics provides deeper insights: there is a theorem from physics and geometry that to each symmetry there is a conserved motion, which in this case is the angular momentum. It can be shown that the law of sines in trigonometry is a consequence of this conservation law. It is a further attribute of differential geometries that there will also be two associated forces: a centripetal scalar force and a Coriolis vector force. Identifying symmetries provides substantial insight into the geometry. In many cases, the symmetries are not immediately evident, though the attributes are. Locally, we may notice the Coriolis forces before we notice that the earth is not flat.

We also believe that there are important “symmetries” in decision-making, though as with the curvature of the earth, it may be that the attributes or consequences of the symmetries are more noticeable than the symmetries themselves. We find it notable that the game theory approach to decision-making uses the Nash equilibrium, a static scenario in which each player considers his or her version of the game, considers all the worst consequences that can happen, and from those chooses the best of the worst. It is often framed as a max-min choice. It is an equilibrium in the sense that every player makes the same type of choice, and no other choice works better for any player.

The idea we take away from this is that first, it is idiosyncratic: it is based on each player’s personal view of the utilities. Second, the max-min choice has relevant mathematical connections to geometry: the dynamic path or motion in a rotating frame has one “equilibrium” direction parallel to the rotation axis, which can be framed as a max-min solution to motion. Motion in any other direction will be influenced by apparent or Coriolis forces. For this talk, we don’t go into detail other than quoting the result that if we associate with each player a symmetry, then the consequence will be that there will be a game matrix associated with that player that dictates the relative utilities and there will be an equilibrium set by a max-min choice.

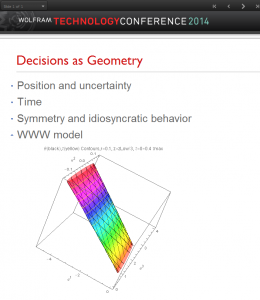
WWW model: with these preliminaries of geometry out of the way we can briefly describe the decision model we will use as an example of complicated geometries. We call it the Work-Wealth-Wisdom model. The various figures or CDF models, such as the one above, have been computed based on the explicit model and numerical values chosen.

One common way in game theory to formulate a decision is to specify a matrix that indicates the payoffs. The rows correspond to the choices of one player and the columns the other player. From a mathematical perspective, this can be reformulated as a symmetric game in which the rows specify the choice of every player plus one additional row called the hedge strategy, and the columns also specify the choice of every player and one additional column called the hedge strategy.

This is the symmetric version of the payoff strategy for the WWW model. The model shown here is totally illustrative and the numerical values could be chosen quite differently. There are two players: the work-player and the wealth-player. Wisdom is how they play the game. The order of the rows (columns) reflect the wealth-player (player 2) strategy to invest wealth into the economy or to collect rent, then the work-player (player 1) strategy to earn or to “take” money, then finally the “hedge” strategy that we identify with time.

The model incorporates the idea that wealth has 10 times more value than the work and the consequence is that there are 10 times more workers than wealthy. The payoff to the worker is 1 if their choice is “work” and the wealth choice is “invest”. The worker gets nothing if the wealth choice is to collect rent. The payoff to the worker is 0 if the worker chooses to “take” and the wealth choice is “invest”. The payoff is 1/10 if the wealth choice is to “rent”. In the sense of game theory, no pure choice forms an equilibrium. The best choice for the work-player is to pick either choice with a 10:1 choice favoring “take”. The best choice for the wealth-player is a 10:1 choice favoring “collect rent”. From the standpoint of game theory, this is where we stop, except that we have a second game matrix for the wealth-player that is in principle independent. That is the sense that the choices are idiosyncratic.

In a decision geometry, the symmetric payoff matrix is in fact a rotation in the space of strategic decisions consisting of the two choices for the work-player, two choices for the wealth-player, two hidden dimensions reflecting the symmetry which generates each of the two payoff matrices and time. The space is seven dimensional, in which only five of the dimensions are “active” or not hidden. In our model, we assume that the sum over all the active strategies is a symmetry, leaving us with a four dimensional world in which three are “space” and one dimension is “time”. The model is thus parallel in some respects to the physical world we live in. This is purely for numerical convenience and helps us visualize what is going on more easily.

Geometry: It is worth noting that the concept of payoffs arises entirely from an inquiry into utility and economic behaviors. However from a mathematical point of view, we see it as a hint of an underlying geometry. It is possible to use mathematics to relate the payoffs to a concept of distance between points in this strategic space-time. We thus move the ideas above from a concept of coordinate strategic surfaces to the concept of a function of such coordinates that define a distance function on the space-time manifold. The payoffs are then just one aspect of this distance function. This is the context in which we view decisions as geometry.

Visualization: The resultant geometry is one whose structure changes over time in a well-defined way. Our challenge is to describe that change in a way that makes sense and can be pictured. An example may help: the surface of the ocean is an example of something whose shape changes as a function of time. On the one hand, in the normal coordinates of viewing, we see the shape constantly changing. On the other hand, there are behaviors that can be more simply described if we imagine we are a cork riding on the surface: from our co-moving perspective everything is stationary, though we see structures that when related to the normal coordinates appear as dynamic structures such as waves. We find the same is true in our general geometry. There are many types of solutions, some of which allow a co-moving description that is stationary. Though stationary or steady-state, the motion described is still dynamically interesting: we get standing waves for example. The steady-state motion is what happens after all transient effects die out. For the WWW model, we have positions in the co-moving frame that we call x, y and z as well as a proper time ${\tau}$ . These relate back to normal coordinates of 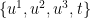$\left\{ {{u}^{1}},{{u}^{2}},{{u}^{3}},t \right\}$ . This will be our first type of visualization.

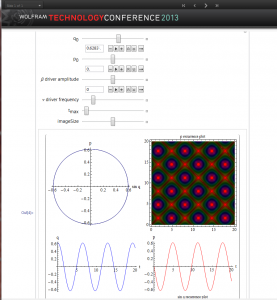
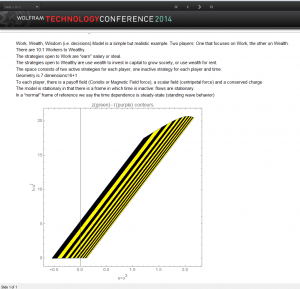
So for example with x and y constrained to be on a circle with fixed radius and arbitrary angle (a cylinder), we can ask what that behavior looks like in normal coordinates. That is shown above. We can also look at the velocity flow, 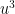${{u}^{3}}$ against t, as contours as shown below. For the WWW model, the income inequality generates a corresponding velocity. What are the normal coordinates here? 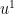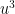The direction ${{u}^{1}}$ is the relative preference for “work” versus “take”; the direction ${{u}^{2}}$ is the relative preference for “invest” versus “rent collection”; the direction ${{u}^{3}}$ is the relative intensity with which each player plays the game, work minus wealth. So in the graph below, the vertical axis is time and the horizontal axis is 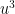${{u}^{3}}$ . The strong direction along the horizontal axis reflects the increase in workers needed because of the assignment of value to wealth. This was put in as an initial condition; the model then shows the consequence of this assumption over time. Note that co-moving time contours are not constant in normal time. This reflects our way of dealing with time as similar to that of Maxwellian and not Newtonian theories.

Steady-State Solutions

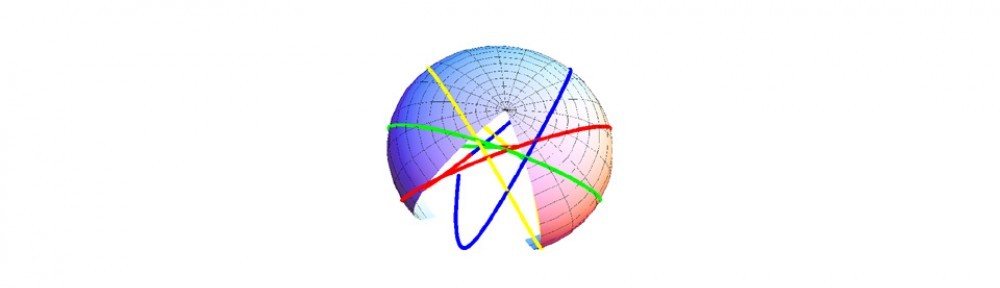
One way to characterize a geometry is by how one measures distances. For example we may use flat maps to plot a course over the ocean. On this map, the latitude and longitude may appear as orthogonal straight lines. However for an accurate course, we need to know how to relate these lines to distance; if we go far enough the distance is not Euclidean since the earth is approximately an oblate spheroid. Another way to characterize a geometry is to plot the paths that represent the shortest distance between two points. It is derived from the distance measure and reflects the curvature of the space. Thus, we may study the complexity of the geometry either by the shape of the surface or by the shortest paths. A complicated geometry is one in which the paths are complex. An example from weather might suggest what we have in mind: a hurricane or tornado both have cyclonic paths of wind, suggesting chaotic behavior. Ordinarily we associate chaotic behavior to the time dependence of the flow. Yet we can have cyclonic behavior that appears stationary. A good example of such a flow is the “spot” on Jupiter that has been around for centuries. In this talk we focus on such steady-state behaviors that remain after any transient effects die out. Of course there will also be behaviors associated with the transients, but they are the subject of a future investigation.

We suggest that the origin of complex behaviors, such as chaotic behaviors, are similar in different domains of study, be they weather phenomena, electromagnetic phenomena or decision phenomena. In each case there are symmetries that give rise to Coriolis forces, magnetic forces or payoff forces respectively. These forces arise from common differential geometry structures.

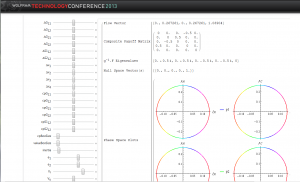
To study these structures we would start with the fact that the cyclonic behaviors are the result of rotations and such rotations can be investigated by looking at the fields that generate the rotations. The following shows a “phase space” plot of the fields from the WWW model that are used to generate the overall payoff matrix.

This field is anything but simple. The CDF picture can be rotated showing the type of complexity one might get. For the experts, we note that this picture is the set of limit surfaces for the z component of the gauge field, along with the partial derivatives of that gauge field along the other two transverse directions x and y. A sphere would be the 3-dimensional analog of a circular phase space plot in 2-dimensions , which is quite different from what is shown here.

Steady-State Solutions can be chaotic

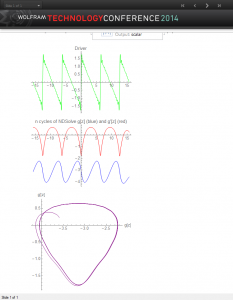
Of course the solutions that we obtain for a geometry may depend on the assumptions used to do the numerical work. So we take a step back and analyze the types of assumptions that we have made. Our tentative conclusion is that we can apply a “harmonic-series” approximation and still identify chaotic solutions. This follows from a technical discussion using Mathematica as a computational tool.

Consider a gravitational source equation with non-linear terms:

${{g}''\left( z \right)+\sin g\left( z \right)=F\left( z \right)}$

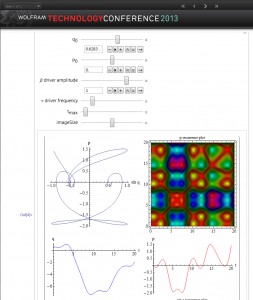
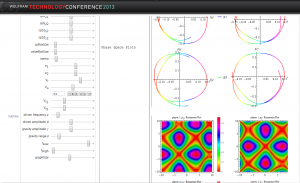
The source, which is the first figure above (green curve) is periodic and for illustration is a saw-tooth pattern. We scale it by a factor, init, which we vary. The equation is solved using NDSolve from Mathematica using periodic boundary conditions. It uses the method of lines to compute the function, red curve, and its derivative, the blue curve. For a sufficiently small factor value of init, the phase space plot shown in purple is a closed cycle. However past a critical value, the non-linear nature of the equation asserts itself and we cease to have closed cycle. We suggest this is the start of chaotic behavior, though we haven’t used a rigorous definition to establish this suggestion yet. The factor value chosen in this figure is init=1.7.

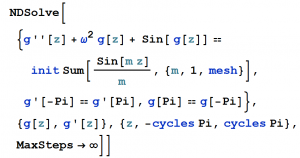
Use Manipulate to make chaotic behavior visible

The Manipulate function in Mathematica is a way to explore when the phase space plot ceases to be a limit cycle. We have considered different source terms, and in particular explored approximating the saw-tooth behavior as a Fourier series with a finite number of terms.

We need not extend the harmonic approximation to the solution. As noted above we use the methods of lines to obtain our full result. For more general geometries, we have also use periodic boundary conditions for all but one space direction. For time, we have considered a single Fourier frequency. For the remaining space direction we use NDSolve and the methods of lines.

General geometries however, may impose differential constraints on initial conditions. On the initial boundary we may have to solve a differential equation in one or more dimensions. The boundary conditions we may need to impose may also be periodic. Now however, the method of lines may not work if there are two or more independent coordinates. So what do we do?

Our solution was to expand the unknown functions as a harmonic series with unknown coefficients. We then substitute the function and its derivatives into the differential equations and use FindRoot to obtain the numerical values of the coefficients. In one dimension we can also use the method of lines as a comparison.

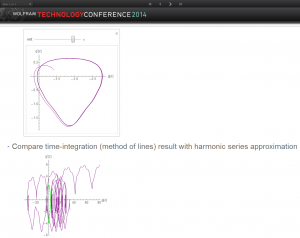
So, returning to the simple gravity source equation above, with a clearly chaotic behavior, purple curve, we also solve the same system using the harmonic approximation, green curve. Not surprisingly, the harmonic approximation is always a limit cycle. We see that the cycle fits into the more general solution. By changing the start point for FindRoot, we have found other limit cycles. So the chaotic behavior manifests itself in the harmonic approximation as multiple solutions.

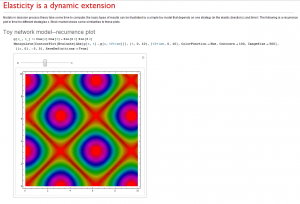
For the decision geometry WWW model, using the harmonic series approximation, we get the limit surface, that we described earlier:

That it is a surface and not a hyper-curve is a consequence of it being a harmonic series approximation. However, the specific surface may depend on the “sources”.

Steady-state analysis: We can now describe more fully the steady state analysis that we perform for differential geometries. We illustrate the technique using an example in one time and one space dimension:

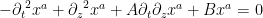
$-{{\partial }_{t}}^{2}{{x}^{a}}+{{\partial }_{z}}^{2}{{x}^{a}}+A{{\partial }_{t}}{{\partial }_{z}}{{x}^{a}}+B{{x}^{a}}=0$

This form of a “wave equation” is typical of the harmonic gauge choice that is always possible to make in a differential geometry. The concept of steady-state is similar to that in electrical and mechanical engineering: As long as the functions A and B are functions only of the space variable z, we can replace the coordinate function with the product of a harmonic in time and an unknown function of space:

${{x}^{a}}={{g}^{a}}{{e}^{i\omega \tau }}$

In other words, the harmonic gauge is then a linear equation in the coordinate. This reduces the partial differential equations to one of lower degree, one that is elliptic and depends on the frequency chosen. It has the form:

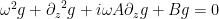
${{{\omega }^{2}}g+{{\partial }_{z}}^{2}g+i\omega A{{\partial }_{z}}g+Bg=0}$

When there is more than one spatial dimension, the coefficients A and B depend on the coordinate so these become coupled elliptic partial differential equations. An example is the three spatial dimension model with one time:

This steady-state solution could be viewed as a solution to a model from general relativity, decision process theory, or in fact any differential geometry model with three space and one time dimension. The boundary and initial conditions, however, will be specific to the problem domain.

We solve these equations using NDSolve, periodic boundary conditions for all but one spatial direction, and use the method of lines for the remaining direction. Constraint differential equations for the coefficients on the initial surface (all spatial directions but that reserved for the method of lines) will be solved using the harmonic series approximation to ensure that the coefficients remain periodic on the boundary.

Based on our investigations to date, we expect that the resultant solutions have the possibility of exhibiting not only “linear” and “near linear” solutions corresponding to simple limit surfaces, but more complex behaviors corresponding to chaotic-type behaviors such as space filling curves. We hope to be able to investigate what we believe is a quite rich structure embedded in these differential geometries. Our remaining examples will be taken from decision process theory, and in particular from the WWW decision model. We will focus on only two aspects out of what is in fact a vast wealth of possibilities: time and communication.

Decision geometry is more complicated than Newtonian physics

We start with a consideration of time and what it means in a differential geometry that consists of a generalized notion of time and space. We have a number of questions:

Which way does time flow? Yes we know it increases and we know it moves in some sense orthogonal to space, but in which direction is that?
- Do we define the direction of time flow along the normal to the surface of constant time?
- Do we define the direction of time as being orthogonal to a spatial volume element? The volume, $dx\wedge dy\wedge dz$ , is the wedge product generalization to the “cross product”
Are these two directions the same or different in a general geometry
Which way are they in the WWW model?
How does the velocity we call 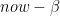$now-\beta$ help us understand and visualize the distinctions?

Time direction: In Newtonian physics, the physics that perhaps comes closest to the way most of us were raised, time clearly moves forward and never backward. Moreover, it is clear that time is orthogonal to all of the directions of space: up and down; forward and backward; left and right. Starting from this perspective, we construct our geometry, which is Euclidean in nature. Time flows and has a value that is the same everywhere in space. We have no real evidence of course that this is true. In fact, modern physics experiments demonstrate that this is not true. It is not that our ideas are unfounded, but that we have attempted to extrapolate our ideas too far beyond what we have observed.

We observe time locally, just as we measure distances in space locally. In our current location, what we mean by a coordinate is a value that is the same in a small region around where we are, at the current time. What we mean by time is a small region around where we are where a common clock suffices to provide a value for the current time. Putting these ideas into mathematics is brings us to differential geometry. In this discipline, we talk about a surface on which a coordinate is constant. Such surfaces exist at each point and extend to a region around that point. The region is not arbitrarily large however; it depends on the curvature and topology of the space. For a Euclidean space-time, the region does in fact extend everywhere. For curved space this is not the case.

Normal time: From this mathematical perspective, we might then define the direction of time at each point as being along the normal to the coordinate surface associated with time at that point. For the steady-state WWW model, we can say more. The flow in that model is stationary in the co-moving frame. So at each point, we can say that the normal of the time surface is along that flow; the flow is moving at a certain velocity, which can be normalized as the ratio of the co-moving space component of flow divided by the co-moving time component of flow:

${{\beta }_{\upsilon }}=\frac{{{E}^{t}}_{\upsilon }}{\sqrt{1+{{e}^{\alpha }}{{e}_{\alpha }}}{{E}^{t}}_{o}}$

This is the 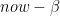$now-\beta$ . The additional square root in the denominator accounts for the energy due to the inactive component of flows that are associated with the idiosyncratic symmetries. The subscript in the numerator reflects the co-moving space components; the subscript in the denominator reflects the co-moving time component of flow.

We denote the co-moving directions as x, y and z; z is the direction in which we use the method of lines and the other two directions are transverse in which we use periodic boundary conditions. It is thus very natural to consider not x and y, but the radial directions such that

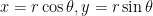
$x=r\cos \theta ,y=r\sin \theta$

Using this notation, we can fix the radius to a number and look at solutions for all angles. We thus map a cylinder in the co-moving space into a two-dimensional surface in the “velocity” space associated with one concept of time.

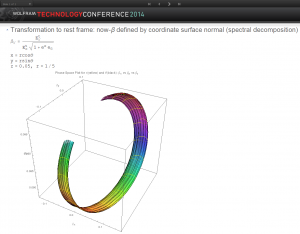
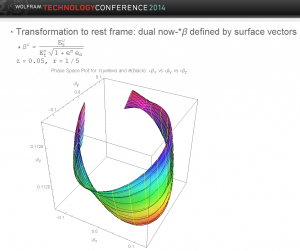
The image above shows this surface for r=0.2 and z=0.05; the CDF file provides an interactive way to view the same surface.

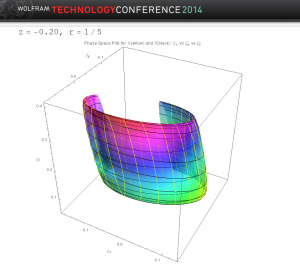
This figure shows the “velocity” surface at a different point, r=0.2 and z=-0.20. The two surfaces are quite different. If the flow were the same at every point, we would conclude that the geometry and time flow reflect some simple property such as the system is moving uniformly without rotation. This is clearly not the case.

Orthogonal time: Now let’s pursue a different approach, which is to consider that time flows in a direction normal to the space. To give this meaning, note that we are used to considering a small volume of space at each point and associating physical facts to such volume; the volume itself, the mass contained on that volume, the total utility associated with that volume, etc. Differential geometry also considers volumes, starting from the notion of a surface spanned by two coordinates, say x and y. The normal to the surface for x is a differential change dx; similarly the normal to the surface for y is dy. The surface area however spanned by dx and dy is related to the product, called the wedge product between the two: 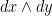$dx\wedge dy$ . It is the anti-symmetric product of the two vectors. The volume is the wedge product of any three independent normals: $dx\wedge dy\wedge dz$ . It is the anti-symmetric product of all three.

In differential geometry, we form the dual to any wedge product by a rule that constructs a totally anti-symmetric product of the given wedge product and adjoining all the remaining directions in an anti-symmetric way. In a four dimensional space-time, the dual of the volume is a one dimensional vector:

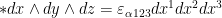
$*dx\wedge dy\wedge dz={{\varepsilon }_{\alpha 123}}d{{x}^{1}}d{{x}^{2}}d{{x}^{3}}$

In general, hyper-volumes are described by forms. They generalize the cross product to higher dimensions. In particular, the direction orthogonal to the volume also provides a direction for time, “orthogonal time”. We can move along orthogonal time to get to the co-moving frame, but we must use the dual flows, suitably defined with the above dual operator: $now-*\beta$ :

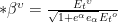
${*{{\beta }^{\upsilon }}=\frac{{{E}_{t}}^{\upsilon }}{\sqrt{1+{{e}^{\alpha }}{{e}_{\alpha }}}{{E}_{t}}^{o}}}$

The orthogonal time gives a velocity surface above for the $now-*\beta$ that is quite different from before for r=0.2 and z=0.05. It visually evident from the shape and not just from the numbers; though the numbers are quite different as well.

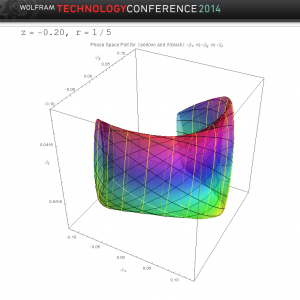
As before, the shapes are not the same at different points. Here is the point r=0.2 and z=-0.20. It is instructive to rotate these shapes and explore their detailed characteristics.

We seem to conclude that time is not an absolute, but a quantity that has some substance. It can be viewed in a variety of ways and shows different characteristics from what we are used to from Newtonian physics. The images here from Mathematica help visualize these differences. They arise from the different ways we can view the flow to a co-moving frame.

Communication has a finite speed

Closely associated with time is the speed with which events communicate with each other. We certainly know that this communication is not instantaneous. Nevertheless, we have that idea from Newtonian physics and it is built into our way of thinking. It is hard to contemplate the consequences that communication has a finite speed. Communication is information flow and certainly a great deal has been written on that subject. From a causal point of view, what can we say?

From our study of physics, we learn that Maxwell had it right about communication. Light, in that theory, always travels at the same speed. This is surprising since it means a beam of light originating from a train travels no faster or slower than one on land as the train passes it. This is not in conformance with our notions of relative speed from Newton. It was this idea that was modified by Einstein. It certainly impacts our way of thinking about differential geometries, since some will behave in a Newtonian fashion and others in a Maxwellian fashion. It is our choice to pick the latter.

The consequence is that we view space as Riemannian and that there will be an analog of “light” that will travel at the maximum speed, corresponding to a zero path length:

$d{{\tau }^{2}}={{g}_{mn}}d{{u}^{m}}d{{u}^{n}}+2{{g}_{mt}}d{{u}^{m}}dt+{{g}_{tt}}dtdt=0$

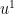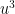In this expression the coefficients are summed over the spatial indices m and n. For example in the WWW model, the sums go from 1 to 3 and the direction ${{u}^{1}}$ is the relative preference for “work” versus “take”; the direction ${{u}^{2}}$ is the relative preference for “invest” versus “rent collection”; the direction ${{u}^{3}}$ is the relative intensity with which each player plays the game, work minus wealth.

The idea that communication travels at a finite speed makes sense for any theory about our world, not just physics. But it has consequences when translated into differential geometry. There is a presumed measure of distance or metric between any two points given by the above rule. There is thus a relationship between the velocities or flows for maximal communication set by the surface in terms of this measure or metric:

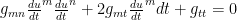
${{{g}_{mn}}{{\frac{du}{dt}}^{m}}{{\frac{du}{dt}}^{n}}+2{{g}_{mt}}{{\frac{du}{dt}}^{m}}dt+{{g}_{tt}}=0}$

What this means is that the maximum communication flow must lie on this ellipsoid. All communications must lie inside. This imposes constraints on the possible values of the metric elements, which must vary continuously from their initial values.

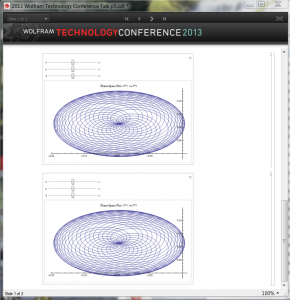
Here is a sample surface computed from the WWW model at a point. As one moves from point to point, the shape changes shape and can in fact turn into a hyperboloid. In Mathematica we use Manipulate to study this. A hyperboloid allows communications that occur at zero speed or infinite speed, neither of which are reasonable. Since the coefficients of the ellipsoid, the metric elements, are computed from the differential geometry equations, there are constraints on these metric elements.

We can gain additional insight by considering not just the velocity flow of communication, but the dual normalized 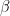$\beta$ -flow:

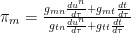
${{\pi }_{m}}=\frac{{{g}_{mn}}\frac{d{{u}^{n}}}{d\tau }+{{g}_{mt}}\frac{dt}{d\tau }}{{{g}_{tn}}\frac{d{{u}^{n}}}{d\tau }+{{g}_{tt}}\frac{dt}{d\tau }}$

It is the dual of the communication flow. We argued above that there was a difference between flow velocities related to the space and its dual. The dual was related to flows that we distinguished by whether the indices were upper or lower. Again, we are making that distinction here, to help us remember that this is not the flow but a linear combination of flow components. The requirement that communication be finite can be written in terms of these components and the inverse of the metric:

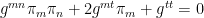
${{{g}^{mn}}{{\pi }_{m}}{{\pi }_{n}}+2{{g}^{mt}}{{\pi }_{m}}+{{g}^{tt}}=0}$

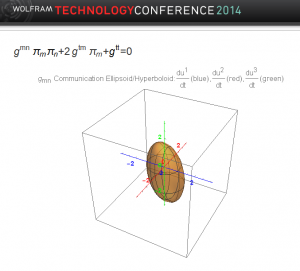
This shows the result for an initial point for the WWW model. Again, as we move away from this initial point, we require that the shape stay an ellipsoid. If we get zero or infinite 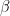$\beta$ flow, this is not physical. As before actual communication lies inside this ellipsoid. This imposes constraints on the inverse of the metric formed from the metric matrix elements 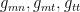${{g}_{mn}},{{g}_{mt}},{{g}_{tt}}$ . Checking that we maintain the communication ellipsoid and its dual is easy and intuitive.

Summary

We have indicated several concepts that are distinct when we move to more complex geometries:

Steady-state solutions can be more complex
- limit surfaces that are complex
- Chaotic behaviors
Visualization challenges
- Dimensionality
- Gauge Invariance
- Conservation laws (symmetries)
- Normal versus orthogonal time
- Finite communication speed
- Communication ellipsoids
Application to decision geometry
- WWW model
- Provides insight into decision-making
Applications apply equally well to general relativity
Speculation: can one extend these ideas to engineering?
- Especially the ideas of harmonics and harmonic series approximation

Wolfram Technology Conference 2013

Posted on December 25, 2013 by Jerry

The following is based on the talk given at the 2013 Wolfram Technology Conference held October 21-23, 2013. The talk was presented as a Wolfram CDF slide show and is reproduced here along with segments that can be executed using the free Wolfram CDF Reader. Since the slides don’t capture everything that was presented, I have also provided additional commentary.

Introduction

This talk continues an inquiry into the relationships between decision making, determinism and chaos: an initial in-depth exposition can be found on this site. Decision making is one of the most human acts and seems to be the most difficult area to formalize into a theory of behaviors that are causal and deterministic. In fact one might think that the very nature of decision making is one of chance and uncertainty. One issue we think relevant is a lack of appreciation on how causal theories deal with uncertainty. In the view of many, there is insufficient understanding of the sensitivity of the dynamic behavior on the initial conditions. When these issues are taken into account, it becomes easier to see the possibility for causal formal theories of human decision making. See a related and much earlier MIT paper on this subject based on Systems Dynamics, Sterman et al.

One thing that might help our understanding of these issues is to explore how we deal with uncertainty in such mundane activities as measurements, which form the basis of physical theories. So for example, we understand by length, an attribute that characterizes the height, width or depth of something. It is a great accomplishment in understanding to separate this concept from the mechanisms by which we perform the measurement. The mechanisms involve a measuring stick and us as agent; for those of you measuring a basement, you know that multiple measurements yield multiple answers. Yet we are confident that the basement has well defined dimensions. How did we come to this conclusion and how did we learn to separate out the uncertainties associated with us as agent and the intermediary of a measurement stick, from the invariant concept of length? I think we all agree that the separation has been done and we are comfortable with the idea of length.

This distinction in measurements can also be made when making decisions. There are aspects of decisions that are uncertain which mask potential underlying relationships that are causal. As an example I may choose between several strategies according to a fixed set of frequencies that behave according to a deterministic causal theory, yet there can still be an uncertainty in measuring the exact numerical values of these frequencies. More importantly I may not know what choice I will make at some future time even though the frequency of choices is known. There is no requirement that a causal theory of decisions needs to address that issue. Indeed to construct a causal and deterministic theory we may be better off not including such uncertainties in our theory, just as in physics we are better off not including the measurement process. Such processes are usually treated as stochastic with no dynamic structures.

We distinguish such measurement uncertainties from the dynamic uncertainties that result from sensitivity to initial conditions. The latter lead to chaos, showing that deterministic causal theories can have rich dynamic structures with understandable regularities, in contrast to stochastic behaviors. To present these important concepts we proceed as follows:

introduction
decision making
determinism and chaos
elasticity
determinism and chaos in decision theory
fixed frame models–complete solutions
conclusions

Decision Making

We note that many decision making behaviors that appear to be uncertain may well have causal elements. For example the behavior of the stock market, which is clearly an example of decision making, appears often to have elements that are uncertain. However if we observe the time series behaviors of the stock market using recurrence plots, we see causal systematics:

Here we have captured the behavior of a particular stock using Wolfram Alpha and created its recurrence plot. The details can be found in the CDF file, which allows the reader to further explore such plots using different stocks.

Determinism and Chaos

The other extreme of uncertainty would be to consider behaviors in the physical world which are assumed to follow well understood laws. A simple example can be taken from physics and the motion of a pendulum. Here non-linear spatial behaviors can also manifest as non-linear time behaviors, including behaviors called chaotic.

Without making a small angle approximation, for low amplitudes the behavior is periodic. There is no structure. However, the force on the pendulum is not proportional to the angle but to the projection of the force along the vertical direction. This introduces a non-linearity. The consequence can be highlighted in a number of ways. One is to provide a oscillating harmonic force on the pendulum. Alternatively, one can start the pendulum with an initial but large velocity. Here is a typical result.

The CDF file allows the reader to experiment with different initial conditions and different values for an external harmonic force. One of the consequences of this deterministic behavior is chaotic behavior. By this we mean that the behavior depends sensitively on the initial conditions. Even though the equations are causal the resultant behavior appears uncertain; in reality the uncertainty is an artifact of the initial conditions, not of an underlying uncertainty in the physical process. The underlying dynamics impose regularities on such chaotic behaviors that have been extensively studied. There is an inter-play between what happens in space and what happens in time. We believe such interactions also occur in decision making.

Elasticity

We believe that decisions have not only a causal connectivity but a strategic connectivity. We adopt conceptual game theory that decisions are characterized by players or agents that each decide from a list of pure decisions, assigning a frequency of choice to each. From a mathematical perspective each game is decided by these frequencies which represent a point in this space of strategies, spanned by all possible frequency choices. we focus on games which are played multiple times so that we observe both the time evolution and the spatial connectivity. The hypothesis is that decisions change continuously in time and strategy space. We call connectivity in time causal. We call connectivity in strategic space elastic. Spatial elasticity may be related to network connectivity, whose importance is argued by Barabasi.

Game theory, as opposed to our restricted version of conceptual game theory, usually deals with an equilibrium situation, so the idea of causality and elasticity are outside of the scope of the theory. They enter indirectly in the problem statement. We make arguments about the payoffs, which are the key elements of the theory that lead to a specification of the strategic frequencies at equilibrium. what we ordinarily don’t do is assume that the payoffs can change over time. We also don’t consider the possibility that the payoffs and the frequencies are not simply tied by an equilibrium condition.

To explore how this works, we can take any game and see how various decision attributes such as payoffs and frequencies might change over time. We can use the sliders in the CDF model to simulate time. As an example we take the children’s game of rock, paper scissors.

In practical terms, a way to do better in the game is know something about your opponent. If they don’t like playing certain strategies, you are better off adjusting the payoffs to reflect that. As they learn about your behavior, they adjust their behavior causing you to readjust your behavior. You can experiment with the above model to see the effects. In this picture, we assume that the payoffs are in fact given by their equilibrium values. Shortly we remove that restriction.

What we learn from this is that there are degrees of freedom that can change independent of time. We call it space as an abuse of language: we mean strategic space, not physical space. We anticipate that changes in space will influence changes in time. A simple model to illustrate a network model with elasticity is the following:

If you change the spatial variable, the time recurrence pattern changes. It illustrates what we see in the general theory without the corresponding mathematical complexity. The key concept we propose is that decisions are causal and elastic: they depend jointly on time and space variables. Because of the interconnectivity, the resultant behavior is analogous to an elastic medium, which can exhibit waves that propagate, reflect and possibly die out. This goes beyond game theory as well as simple Systems Dynamic models. We now make these ideas more precise.

Determinism and Chaos in Decision Process Theory

Just as in physical models, we have a causal dynamic model in mind. We take these ideas from decision process theory and the behavior along a streamline:

We start with a set of equations:

The first equation sets the rate of change of the frequencies that determine strategic choice. On the left is the rate of change of those changes and on the right is the effect on those changes based on the payoffs. When the payoffs are zero, the rate of change on the left is zero. We consider more general changes here. The second and third equations determine the response of the equations to harmonic forces, analogous to those for the pendulum.

Time dependence occurs in the above equations even if the payoffs are independent of time. We see that the frequencies no longer are constants but may oscillate and exhibit other dynamic behaviors just because we are no longer at equilibrium. Shortly we will also consider the possibility that the payoffs also vary in time. But for now assume that they are constant.

We consider a prisoner’s dilemma model in which we can change the various parameters that govern the payoffs. In addition we can change the relative weights of the payoffs for each player, which can introduce non-linear effects independent of the harmonic forces.

When we have small oscillations away from equilibrium, as with the pendulum we see harmonic behaviors for all of the strategies as seen above.

However as we either add more harmonic forces or move away from small oscillations, non-linear behaviors result as shown above. We get chaotic behavior for some choices of the parameters. One can play with the details using the CDF model.

Fixed Frame Models–Complete Solutions

The other source of causal and elastic behavior occurs when the payoffs can also vary. Decision process theory provides for that possibility. There is a soluble model (numerically); the one we choose is an attack-defense model. With a suitable choice of parameters, we again observe non-linear behaviors:

In these figures, there are four possible strategies in an attack-defense war game in which one side defends two targets (one high value one low value) and the other side can attack the two targets. The standard game sets payoffs for the four cases. We no longer assume here that the game is played at equilibrium. We assume only that the sum of strategies (actually preferences in the theory) is conserved, leaving three strategies that can vary. Along a streamline, we view the behaviors of the payoffs as functions of time and three parameters that characterize the strategies along the streamline: x, y and z in the figure. Using sliders we can see how the phase space plot changes. This model is somewhat more complicated and is too large to provide in this talk. So in this case we just provide a couple of illustrative examples.

We see the same type of qualitative behavior as before, without making any assumptions about the form of the harmonic force; it is an outcome of the theory in this case.

Conclusions

In general, chaotic effects require non-linear behaviors. We have observed such behaviors in a decision process theory and expect to see such behaviors in realistic decision processes, including stock market behaviors. These behaviors depend on both causal and elastic effects. The new ingredient is paying attention to the elastic components of decisions: both payoffs and frequencies can vary in time and strategic position.

Decision making chaos and determinism

Posted on June 12, 2013 by Jerry

This is an inquiry into decision-making and its connection to uncertainty. It is based on the white paper with the same title. Decision making is one of the most human acts and seems to be the most difficult area to formalize into a theory of behaviors that are causal and deterministic. In fact one might think that the very nature of decision-making is one of chance and uncertainty. One issue we think relevant is the general lack of understanding of causal theories and how they deal with uncertainty. Moreover, in our view, there is insufficient appreciation of the sensitivity of the initial conditions that determine future behaviors. When these issues are taken into account, it becomes easier to see the possibility for causal formal theories of human decision-making.

Consider the sensitivity of future behaviors on initial conditions, which has been extensively studied under the general category of chaos and chaos theory. It has been said in the past that chaos represents for humans the way we perceive the world in its un-ordered state. If we had perfect information, so the argument goes, we would have perfect determinism. Slight disturbances on what we think we know, lead to unknown consequences, even in a theory that is strictly causal and deterministic. So “what is deterministic?” It seems unreasonable to believe that because chaos behavior is possible, we must throw out our causal theories. They work very well and explain a host of data. We believe that a more reasonable approach is that we must be more careful about what we claim to learn from these causal theories.

The theories after all reflect our efforts to identify concepts and attributes that don’t change with time or that change with time in an understandable, causal and continuous way. One thing to explore is how we deal with uncertainty in such mundane activities as measurements, which form the basis of all physical theories.

So for example we understand by length, an attribute that characterizes the height, width or length of something. It is a great accomplishment in understanding to separate this concept from the mechanisms by which we perform the measurement. The mechanisms involve a measuring stick and us as an agent; for those of you measuring a basement, you know that multiple measurements yield multiple answers. Yet we are confident that the basement has well-defined dimensions. How did we come to this conclusion and how did we learn to separate out the uncertainties associated with us as agent and the intermediary of a measurement stick from the invariant concept of length? Today, we all agree that the separation has been done and we are comfortable with the idea of length.

Similarly, we are comfortable with the concept of time, despite our dependence of using clocks to make time measurements. From such simplistic considerations, we have adopted over many centuries, physical theories of the behavior of matter that we depend on. For example, we are comfortable with a host of physics problems that relate distances objects travel with time. We believe we understand how a pendulum works because we can predict the behavior starting from a description in which we describe its restoring force as being the source of the acceleration. The behavior is the set of positions of the pendulum over time. We start the pendulum at rest and “drive” it by a harmonic force. We predict from Newton’s theory where the pendulum will be at any future moment. We compare where the pendulum is by measurements against where it is predicted to be and find agreement to a high degree of accuracy.

This model, because of the non-linear behavior of the force, generates unexpected structure. In engineering and business, there are also distinct ways to gain access to a system’s non-linear characteristics. For the pendulum, one can initiate the behavior by varying the initial conditions. Alternatively, one can “drive” the behavior by applying an external force. For example we might impose an external force characterized by a single amplitude and a single frequency. As we vary the frequency and amplitude we stress the non-linear structures of the problem. For sufficiently large amplitudes we generate chaotic structures: we go from a quasi-periodic structure to one that no longer appears periodic. We create behaviors that appear much more erratic and lack the periodic behaviors seen with smaller driver amplitudes. The idea is that these properties may in fact carry over into the realm of decision-making.

We expect that decision-making has attributes that involve imperfect information as well as perfect information. The challenge is to identify each of these, separating out those attributes that have a predictable behavior from those attributes that are inherently uncertain. We adopt game theory (Von Neumann & Morgenstern, 1944) in which an intrinsic view of decisions is a productive starting point where we separate out the pure strategies as things of permanent interest. A pure strategy is the complete set of moves one would carry out in a decision process taking into account the moves of all of the other players or agents in the process along with any physical or chance effects that might occur. It is a complete accounting of what you would do, a complete plan given every conceivable condition. It is furthermore assumed that you can approximate this complete list with a relatively small list of pure strategies.

Just because there are pure strategies, there is no reason to believe that one of these pure strategies is the right choice to make. If you are in a competitive situation, there may be a downside to your competitor knowing that you will pick one of these strategies. The solution is to “hide” your choice by picking the pure strategies with a specific frequency. The theory determines for you what these frequencies are without informing your opponent which choice you actually will make on any given play.

Thus your decision choice is a specific frequency choice and in that sense represents the measurement of “length” despite the fact that in a real decision process, like a real measurement process, there are lots of uncertainties. You would like to determine the frequency choices the other players make and they want to understand your choices. We emphasize that knowing these frequency choices is not the same thing as knowing what you will actually do on a given play. We take this knowledge in the same way we take the knowledge about the size of our basement. We know how to get a good approximate set of measurements. We know that out basement has a size. For each measurement process we don’t know what size we will actually get.

We extend game theory to decision process theory (Thomas G. H., Geometry, Language and Strategy, 2006) in which the strategy frequencies vary with time. This theory predicts future frequency values based on a given set of initial conditions. The theory is causal in this sense, without actually dictating what a player will actually do at any given moment. The basis of the theory has some similarities to physics and even more underlying similarities to mathematical models of physical processes. Just as in physics, there can be external forces that dictate how the rates of change of frequencies change in time. There will be stationary situations in which these rates of change don’t change, in which the forces generating such changes are zero. We equate that scenario with the whole literature of game theory and its consideration of static games: the frequencies are fixed numbers. Static games provide an important foundation for our approach, though our results diverge once dynamic effects are included.

A second scenario is one in which the fields that generate the forces are static, but the flows, the rates of change of the frequencies, are dynamic. The flows may depend on what other players are doing, and so we can distinguish a special subset of flows that are stationary: at a specific “location”, the flow doesn’t change. However, if you follow the streamline of the flow you will follow a path that changes in time. You might think of a weather pattern that is stationary, in which the wind at any position is constant in speed and direction. If you follow a path along the wind by adding smoke, you will see that the smoke follows a streamline that moves with time. These considerations are really rather similar to the pendulum problem.

Based on these considerations and verifying our ideas from a variety of numerical examples, we argue that behaviors from decision process theory are deterministic, yet represent the uncertainty of choices based on frequency. We can separate out from the decision process the uncertain aspect of the decision, whose future behavior is unknown: we don’t know which pure strategy will be chosen. Thus we identify that aspect of the decision process that deprives us of perfect information. We also identify those aspects of decisions processes that might evolve continuously in time and can be determined in a causal manner. These are the numerical frequencies of choice that form the basis of the choice, but don’t actually determine the specific choice at any given time. Our theory is then about the frequencies and not about the choices.

This is not the end of the story. Just because we have a theory that determines future behavior based on knowledge of past behavior, we are not justified in assuming that the predictions will be insensitive to our starting point. Non-chaotic behavior assumes that the future behavior is not sensitive to small changes in the starting point. This often follows from theories that are linear in nature. Chaotic behavior by contrast expects small behaviors to generate large behavioral differences, even if that behavior ultimately stays bounded. Over time however, we expect to see significant deviations. Some of the non-linear behavior is a consequence that preferences can’t grow without limits. We postulate that concept here, but in fact do see evidence for that behavior in the full theory.

We expect that chaotic behaviors can be generated from within, without recourse to external “drivers’, if there are suitable parameters that can be varied. For the pendulum, the suitable variable would be the initial speed. The initial flows and payoffs are suitable variables for decision processes. The chaotic behavior is a result of the non-linear nature of the forces and can be made visible with a “driver” representing external periodic forces. It is then a matter of whether the amplitudes and frequencies excite the underlying structures. In fact from both, seemingly benign behaviors as a steady state need not indicate the lack of interesting structures. The key is how to excite these structures into existence.

Decision Process Theory

Decisions are not random, but result from a network of ripples from the past into the future.

Category Archives: chaos

Are there resonant circuits in General Relativity?

WTC-2014: Visualizing behaviors in differential geometries using Mathematica

Wolfram Technology Conference 2013

Decision making chaos and determinism