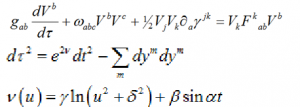Wolfram Technology Conference 2013

Posted on December 25, 2013 by Jerry

The following is based on the talk given at the 2013 Wolfram Technology Conference held October 21-23, 2013. The talk was presented as a Wolfram CDF slide show and is reproduced here along with segments that can be executed using the free Wolfram CDF Reader. Since the slides don’t capture everything that was presented, I have also provided additional commentary.

Introduction

This talk continues an inquiry into the relationships between decision making, determinism and chaos: an initial in-depth exposition can be found on this site. Decision making is one of the most human acts and seems to be the most difficult area to formalize into a theory of behaviors that are causal and deterministic. In fact one might think that the very nature of decision making is one of chance and uncertainty. One issue we think relevant is a lack of appreciation on how causal theories deal with uncertainty. In the view of many, there is insufficient understanding of the sensitivity of the dynamic behavior on the initial conditions. When these issues are taken into account, it becomes easier to see the possibility for causal formal theories of human decision making. See a related and much earlier MIT paper on this subject based on Systems Dynamics, Sterman et al.

One thing that might help our understanding of these issues is to explore how we deal with uncertainty in such mundane activities as measurements, which form the basis of physical theories. So for example, we understand by length, an attribute that characterizes the height, width or depth of something. It is a great accomplishment in understanding to separate this concept from the mechanisms by which we perform the measurement. The mechanisms involve a measuring stick and us as agent; for those of you measuring a basement, you know that multiple measurements yield multiple answers. Yet we are confident that the basement has well defined dimensions. How did we come to this conclusion and how did we learn to separate out the uncertainties associated with us as agent and the intermediary of a measurement stick, from the invariant concept of length? I think we all agree that the separation has been done and we are comfortable with the idea of length.

This distinction in measurements can also be made when making decisions. There are aspects of decisions that are uncertain which mask potential underlying relationships that are causal. As an example I may choose between several strategies according to a fixed set of frequencies that behave according to a deterministic causal theory, yet there can still be an uncertainty in measuring the exact numerical values of these frequencies. More importantly I may not know what choice I will make at some future time even though the frequency of choices is known. There is no requirement that a causal theory of decisions needs to address that issue. Indeed to construct a causal and deterministic theory we may be better off not including such uncertainties in our theory, just as in physics we are better off not including the measurement process. Such processes are usually treated as stochastic with no dynamic structures.

We distinguish such measurement uncertainties from the dynamic uncertainties that result from sensitivity to initial conditions. The latter lead to chaos, showing that deterministic causal theories can have rich dynamic structures with understandable regularities, in contrast to stochastic behaviors. To present these important concepts we proceed as follows:

introduction
decision making
determinism and chaos
elasticity
determinism and chaos in decision theory
fixed frame models–complete solutions
conclusions

Decision Making

We note that many decision making behaviors that appear to be uncertain may well have causal elements. For example the behavior of the stock market, which is clearly an example of decision making, appears often to have elements that are uncertain. However if we observe the time series behaviors of the stock market using recurrence plots, we see causal systematics:

Here we have captured the behavior of a particular stock using Wolfram Alpha and created its recurrence plot. The details can be found in the CDF file, which allows the reader to further explore such plots using different stocks.

Determinism and Chaos

The other extreme of uncertainty would be to consider behaviors in the physical world which are assumed to follow well understood laws. A simple example can be taken from physics and the motion of a pendulum. Here non-linear spatial behaviors can also manifest as non-linear time behaviors, including behaviors called chaotic.

Without making a small angle approximation, for low amplitudes the behavior is periodic. There is no structure. However, the force on the pendulum is not proportional to the angle but to the projection of the force along the vertical direction. This introduces a non-linearity. The consequence can be highlighted in a number of ways. One is to provide a oscillating harmonic force on the pendulum. Alternatively, one can start the pendulum with an initial but large velocity. Here is a typical result.

The CDF file allows the reader to experiment with different initial conditions and different values for an external harmonic force. One of the consequences of this deterministic behavior is chaotic behavior. By this we mean that the behavior depends sensitively on the initial conditions. Even though the equations are causal the resultant behavior appears uncertain; in reality the uncertainty is an artifact of the initial conditions, not of an underlying uncertainty in the physical process. The underlying dynamics impose regularities on such chaotic behaviors that have been extensively studied. There is an inter-play between what happens in space and what happens in time. We believe such interactions also occur in decision making.

Elasticity

We believe that decisions have not only a causal connectivity but a strategic connectivity. We adopt conceptual game theory that decisions are characterized by players or agents that each decide from a list of pure decisions, assigning a frequency of choice to each. From a mathematical perspective each game is decided by these frequencies which represent a point in this space of strategies, spanned by all possible frequency choices. we focus on games which are played multiple times so that we observe both the time evolution and the spatial connectivity. The hypothesis is that decisions change continuously in time and strategy space. We call connectivity in time causal. We call connectivity in strategic space elastic. Spatial elasticity may be related to network connectivity, whose importance is argued by Barabasi.

Game theory, as opposed to our restricted version of conceptual game theory, usually deals with an equilibrium situation, so the idea of causality and elasticity are outside of the scope of the theory. They enter indirectly in the problem statement. We make arguments about the payoffs, which are the key elements of the theory that lead to a specification of the strategic frequencies at equilibrium. what we ordinarily don’t do is assume that the payoffs can change over time. We also don’t consider the possibility that the payoffs and the frequencies are not simply tied by an equilibrium condition.

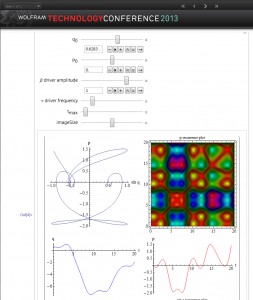
To explore how this works, we can take any game and see how various decision attributes such as payoffs and frequencies might change over time. We can use the sliders in the CDF model to simulate time. As an example we take the children’s game of rock, paper scissors.

In practical terms, a way to do better in the game is know something about your opponent. If they don’t like playing certain strategies, you are better off adjusting the payoffs to reflect that. As they learn about your behavior, they adjust their behavior causing you to readjust your behavior. You can experiment with the above model to see the effects. In this picture, we assume that the payoffs are in fact given by their equilibrium values. Shortly we remove that restriction.

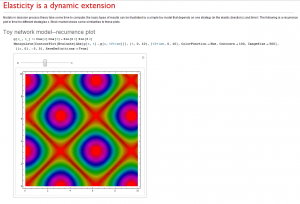
What we learn from this is that there are degrees of freedom that can change independent of time. We call it space as an abuse of language: we mean strategic space, not physical space. We anticipate that changes in space will influence changes in time. A simple model to illustrate a network model with elasticity is the following:

If you change the spatial variable, the time recurrence pattern changes. It illustrates what we see in the general theory without the corresponding mathematical complexity. The key concept we propose is that decisions are causal and elastic: they depend jointly on time and space variables. Because of the interconnectivity, the resultant behavior is analogous to an elastic medium, which can exhibit waves that propagate, reflect and possibly die out. This goes beyond game theory as well as simple Systems Dynamic models. We now make these ideas more precise.

Determinism and Chaos in Decision Process Theory

Just as in physical models, we have a causal dynamic model in mind. We take these ideas from decision process theory and the behavior along a streamline:

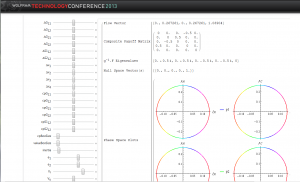
We start with a set of equations:

The first equation sets the rate of change of the frequencies that determine strategic choice. On the left is the rate of change of those changes and on the right is the effect on those changes based on the payoffs. When the payoffs are zero, the rate of change on the left is zero. We consider more general changes here. The second and third equations determine the response of the equations to harmonic forces, analogous to those for the pendulum.

Time dependence occurs in the above equations even if the payoffs are independent of time. We see that the frequencies no longer are constants but may oscillate and exhibit other dynamic behaviors just because we are no longer at equilibrium. Shortly we will also consider the possibility that the payoffs also vary in time. But for now assume that they are constant.

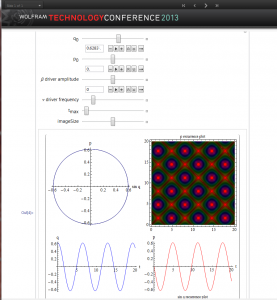
We consider a prisoner’s dilemma model in which we can change the various parameters that govern the payoffs. In addition we can change the relative weights of the payoffs for each player, which can introduce non-linear effects independent of the harmonic forces.

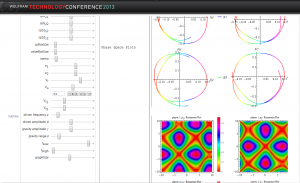
When we have small oscillations away from equilibrium, as with the pendulum we see harmonic behaviors for all of the strategies as seen above.

However as we either add more harmonic forces or move away from small oscillations, non-linear behaviors result as shown above. We get chaotic behavior for some choices of the parameters. One can play with the details using the CDF model.

Fixed Frame Models–Complete Solutions

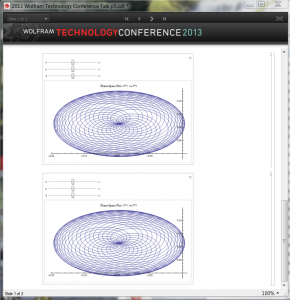
The other source of causal and elastic behavior occurs when the payoffs can also vary. Decision process theory provides for that possibility. There is a soluble model (numerically); the one we choose is an attack-defense model. With a suitable choice of parameters, we again observe non-linear behaviors:

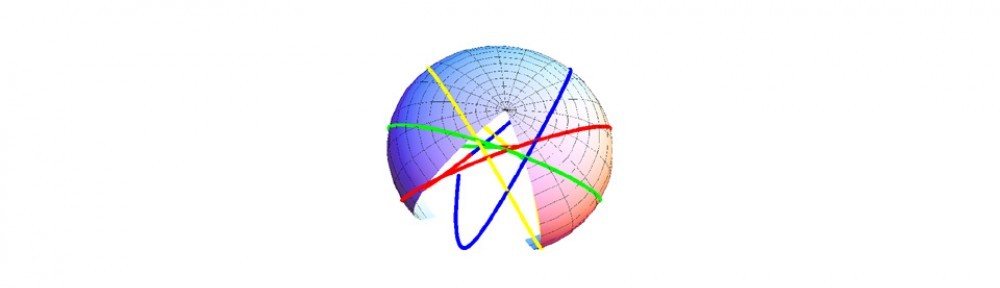
In these figures, there are four possible strategies in an attack-defense war game in which one side defends two targets (one high value one low value) and the other side can attack the two targets. The standard game sets payoffs for the four cases. We no longer assume here that the game is played at equilibrium. We assume only that the sum of strategies (actually preferences in the theory) is conserved, leaving three strategies that can vary. Along a streamline, we view the behaviors of the payoffs as functions of time and three parameters that characterize the strategies along the streamline: x, y and z in the figure. Using sliders we can see how the phase space plot changes. This model is somewhat more complicated and is too large to provide in this talk. So in this case we just provide a couple of illustrative examples.

We see the same type of qualitative behavior as before, without making any assumptions about the form of the harmonic force; it is an outcome of the theory in this case.

Conclusions

In general, chaotic effects require non-linear behaviors. We have observed such behaviors in a decision process theory and expect to see such behaviors in realistic decision processes, including stock market behaviors. These behaviors depend on both causal and elastic effects. The new ingredient is paying attention to the elastic components of decisions: both payoffs and frequencies can vary in time and strategic position.

Decision making chaos and determinism

Posted on June 12, 2013 by Jerry

This is an inquiry into decision-making and its connection to uncertainty. It is based on the white paper with the same title. Decision making is one of the most human acts and seems to be the most difficult area to formalize into a theory of behaviors that are causal and deterministic. In fact one might think that the very nature of decision-making is one of chance and uncertainty. One issue we think relevant is the general lack of understanding of causal theories and how they deal with uncertainty. Moreover, in our view, there is insufficient appreciation of the sensitivity of the initial conditions that determine future behaviors. When these issues are taken into account, it becomes easier to see the possibility for causal formal theories of human decision-making.

Consider the sensitivity of future behaviors on initial conditions, which has been extensively studied under the general category of chaos and chaos theory. It has been said in the past that chaos represents for humans the way we perceive the world in its un-ordered state. If we had perfect information, so the argument goes, we would have perfect determinism. Slight disturbances on what we think we know, lead to unknown consequences, even in a theory that is strictly causal and deterministic. So “what is deterministic?” It seems unreasonable to believe that because chaos behavior is possible, we must throw out our causal theories. They work very well and explain a host of data. We believe that a more reasonable approach is that we must be more careful about what we claim to learn from these causal theories.

The theories after all reflect our efforts to identify concepts and attributes that don’t change with time or that change with time in an understandable, causal and continuous way. One thing to explore is how we deal with uncertainty in such mundane activities as measurements, which form the basis of all physical theories.

So for example we understand by length, an attribute that characterizes the height, width or length of something. It is a great accomplishment in understanding to separate this concept from the mechanisms by which we perform the measurement. The mechanisms involve a measuring stick and us as an agent; for those of you measuring a basement, you know that multiple measurements yield multiple answers. Yet we are confident that the basement has well-defined dimensions. How did we come to this conclusion and how did we learn to separate out the uncertainties associated with us as agent and the intermediary of a measurement stick from the invariant concept of length? Today, we all agree that the separation has been done and we are comfortable with the idea of length.

Similarly, we are comfortable with the concept of time, despite our dependence of using clocks to make time measurements. From such simplistic considerations, we have adopted over many centuries, physical theories of the behavior of matter that we depend on. For example, we are comfortable with a host of physics problems that relate distances objects travel with time. We believe we understand how a pendulum works because we can predict the behavior starting from a description in which we describe its restoring force as being the source of the acceleration. The behavior is the set of positions of the pendulum over time. We start the pendulum at rest and “drive” it by a harmonic force. We predict from Newton’s theory where the pendulum will be at any future moment. We compare where the pendulum is by measurements against where it is predicted to be and find agreement to a high degree of accuracy.

This model, because of the non-linear behavior of the force, generates unexpected structure. In engineering and business, there are also distinct ways to gain access to a system’s non-linear characteristics. For the pendulum, one can initiate the behavior by varying the initial conditions. Alternatively, one can “drive” the behavior by applying an external force. For example we might impose an external force characterized by a single amplitude and a single frequency. As we vary the frequency and amplitude we stress the non-linear structures of the problem. For sufficiently large amplitudes we generate chaotic structures: we go from a quasi-periodic structure to one that no longer appears periodic. We create behaviors that appear much more erratic and lack the periodic behaviors seen with smaller driver amplitudes. The idea is that these properties may in fact carry over into the realm of decision-making.

We expect that decision-making has attributes that involve imperfect information as well as perfect information. The challenge is to identify each of these, separating out those attributes that have a predictable behavior from those attributes that are inherently uncertain. We adopt game theory (Von Neumann & Morgenstern, 1944) in which an intrinsic view of decisions is a productive starting point where we separate out the pure strategies as things of permanent interest. A pure strategy is the complete set of moves one would carry out in a decision process taking into account the moves of all of the other players or agents in the process along with any physical or chance effects that might occur. It is a complete accounting of what you would do, a complete plan given every conceivable condition. It is furthermore assumed that you can approximate this complete list with a relatively small list of pure strategies.

Just because there are pure strategies, there is no reason to believe that one of these pure strategies is the right choice to make. If you are in a competitive situation, there may be a downside to your competitor knowing that you will pick one of these strategies. The solution is to “hide” your choice by picking the pure strategies with a specific frequency. The theory determines for you what these frequencies are without informing your opponent which choice you actually will make on any given play.

Thus your decision choice is a specific frequency choice and in that sense represents the measurement of “length” despite the fact that in a real decision process, like a real measurement process, there are lots of uncertainties. You would like to determine the frequency choices the other players make and they want to understand your choices. We emphasize that knowing these frequency choices is not the same thing as knowing what you will actually do on a given play. We take this knowledge in the same way we take the knowledge about the size of our basement. We know how to get a good approximate set of measurements. We know that out basement has a size. For each measurement process we don’t know what size we will actually get.

We extend game theory to decision process theory (Thomas G. H., Geometry, Language and Strategy, 2006) in which the strategy frequencies vary with time. This theory predicts future frequency values based on a given set of initial conditions. The theory is causal in this sense, without actually dictating what a player will actually do at any given moment. The basis of the theory has some similarities to physics and even more underlying similarities to mathematical models of physical processes. Just as in physics, there can be external forces that dictate how the rates of change of frequencies change in time. There will be stationary situations in which these rates of change don’t change, in which the forces generating such changes are zero. We equate that scenario with the whole literature of game theory and its consideration of static games: the frequencies are fixed numbers. Static games provide an important foundation for our approach, though our results diverge once dynamic effects are included.

A second scenario is one in which the fields that generate the forces are static, but the flows, the rates of change of the frequencies, are dynamic. The flows may depend on what other players are doing, and so we can distinguish a special subset of flows that are stationary: at a specific “location”, the flow doesn’t change. However, if you follow the streamline of the flow you will follow a path that changes in time. You might think of a weather pattern that is stationary, in which the wind at any position is constant in speed and direction. If you follow a path along the wind by adding smoke, you will see that the smoke follows a streamline that moves with time. These considerations are really rather similar to the pendulum problem.

Based on these considerations and verifying our ideas from a variety of numerical examples, we argue that behaviors from decision process theory are deterministic, yet represent the uncertainty of choices based on frequency. We can separate out from the decision process the uncertain aspect of the decision, whose future behavior is unknown: we don’t know which pure strategy will be chosen. Thus we identify that aspect of the decision process that deprives us of perfect information. We also identify those aspects of decisions processes that might evolve continuously in time and can be determined in a causal manner. These are the numerical frequencies of choice that form the basis of the choice, but don’t actually determine the specific choice at any given time. Our theory is then about the frequencies and not about the choices.

This is not the end of the story. Just because we have a theory that determines future behavior based on knowledge of past behavior, we are not justified in assuming that the predictions will be insensitive to our starting point. Non-chaotic behavior assumes that the future behavior is not sensitive to small changes in the starting point. This often follows from theories that are linear in nature. Chaotic behavior by contrast expects small behaviors to generate large behavioral differences, even if that behavior ultimately stays bounded. Over time however, we expect to see significant deviations. Some of the non-linear behavior is a consequence that preferences can’t grow without limits. We postulate that concept here, but in fact do see evidence for that behavior in the full theory.

We expect that chaotic behaviors can be generated from within, without recourse to external “drivers’, if there are suitable parameters that can be varied. For the pendulum, the suitable variable would be the initial speed. The initial flows and payoffs are suitable variables for decision processes. The chaotic behavior is a result of the non-linear nature of the forces and can be made visible with a “driver” representing external periodic forces. It is then a matter of whether the amplitudes and frequencies excite the underlying structures. In fact from both, seemingly benign behaviors as a steady state need not indicate the lack of interesting structures. The key is how to excite these structures into existence.

Decisions: stochastic or deterministic?

Posted on November 25, 2012 by Jerry

We believe we know the answer to the question of whether decision-making is a stochastic process or a deterministic process. It is clearly not deterministic since we, as human beings, have free choice. It is equally clear that some outcomes are far from surprising; in which case the decisions that led up to those outcomes must have played a decisive role. In physics there are similar situations.

For example if I hope to buy carpet for a room, I first take measurements. In one sense the measurements that I get are random because when I do the measurements multiple times, I usually get multiple answers. In another sense however, we have agreed in our society that the room doesn’t change its dimensions at random and ascribe the multiplicity of measurement answers to measurement error. We take the room dimensions as attributes that exist in the “real world” and our measurement errors as attributes of a flawed process. We make no attempt at making a theory of the flawed process but instead focus on theories that deal with what we perceive to be the real world. We justify our approach in noting that the measurements cluster around some average value with a variance that reflects the accuracy of our measurement tool.

A similar point can be made about decision-making. If we focus on the actual choice made at any one point in time, we may be focusing on a process that has sufficient variability from one person to another that a theory of such processes is not practical. However we may focus instead on the frequency with which a person makes choices from a variety of options. In decision process theory, I argue that these frequencies are part of the physical world with enough regularity that we can profitably construct a theory of their behaviors in time. The real world suggests that such behaviors vary continuously in time as well as along all the dimensions that measure preferences.

Since these assertions are about the world we live in, it should be possible to validate whether decision behaviors from one moment to another occur in a deterministic way. A similar question has been asked about certain biological processes, most notably the behavior of heart beats. Since the biology of the heart is very complex and intimately connected with living organisms as opposed to inert organisms, one might conclude that the heart behavior would be stochastic. This turns out not to be the case and is illustrated by considering “recurrence plots” of the time sequence of heart beats $f\left( t \right)$ . One would expect that a contour plot of the heart beats $\left| f\left( t \right)-f\left( {{t}'} \right) \right|$ for different pairs of time would show no structure; one would expect it to look like noise. In fact it shows distinctive structure suggesting that future behaviors of the heart depend on the past behaviors in an organized and continuous fashion.

I propose we look at decision processes in the same way. To illustrate behaviors you might see, I start with a very simple model that displays some of the structures I have seen in numerical evaluation of decision process theory. The simple model emphasizes that the structure I hope to see is not at all esoteric but one that simply has not been noticed much. The important point is that we focus on the behaviors that might follow deterministic rules as opposed to composite behaviors that are mixtures of both deterministic and stochastic effects.

In the simple model I assume two variables, one reflecting time $t$ and the other reflecting some decision preference $z$ . For continuous values of the preference $z$ there is a time sequence, which I take to be given by

$g\left( z,t \right)=\cos z\cos t+\sin 2z\sin 3t$

There is nothing magic about this choice other than I imagine that in the real world there will typically be multiple frequencies in time and that there will be corresponding variations in preferences. The resultant recurrence plot is provided below as a CDF insert. One can vary the preference and see that the structure will in general depend strongly on the preferences, based on the model.

[WolframCDF source=”http://decisionprocesstheory.com/wp-content/uploads/2012/11/ToyDecisionProcessModel.cdf” width=”805″ height=”723″ altimage=”http://decisionprocesstheory.com/wp-content/uploads/2012/11/ToyDecisionProcessModel.cdf”] CDF Figure: Time sequence recurrence plot for toy model for various preference values starting at $z=0$ .

I draw attention to two cases. The first is for $z=0$ in which the single frequency dominates. Seeing periodic behavior in the time behavior of the decision choices would be clear evidence of deterministic behavior. However, it is much simpler than what we would expect from complex structures. The behavior need not be so simple, as can be seen by looking at other values, which display more complex behaviors. To experiment with these behaviors, move the “slider” on the above CDF figure.

This by no means exhausts what we would expect from the real world and by no means exhausts what a realistic theory provides. Decision process theory takes as input time and preference behaviors at some known point. It substantially transforms these inputs into behaviors at all other points of time and preference. Like with physical and geometric theories of this type, the transformations may be essentially linear, in which case the new behaviors look like the old. The transformations may also be non-linear in which case the new behaviors exhibit new phenomena. A simplified process model has been studied extensively by others investigating such new behaviors, as well as looking for complex behaviors, termed creative bios, in physical and biological theories. They have looked for such complex empirical behaviors in physical and biological processes, such as cosmological behaviors of the early universe and the behaviors of heart beats. Causal behaviors (simple and complex) seem to be more common than commonly believed.

Decision Process Theory

Decisions are not random, but result from a network of ripples from the past into the future.

Category Archives: recurrence plots

Wolfram Technology Conference 2013

Decision making chaos and determinism

Decisions: stochastic or deterministic?