Author Archives: Jerry

Dynamic Game: Rock Scissors Paper

Posted on by

The rock-scissors-paper game is simple, with one optimal mixed strategy for each player that consists of picking one of the three choices with equal frequency. The game is fair, favoring neither player. Nevertheless the game has a large following with many claims of how to win at the game.

Decision process theory has something to say here that sheds new light. The perspective is that the payoffs are not fixed for each player; there are negotiation forces that influence the choices to be made not only between players but for the same player. There are also valuation forces pushing the choices along individual strategy directions that need not be “classical game theory”.

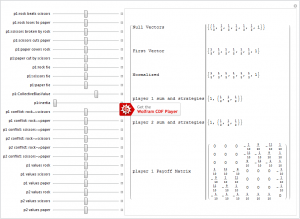
Decision process theory predicts how these forces play out. Without going into the details of the computations, we gain insight into such such forces by analyzing the qualitative aspects of this simple game in the context of the theory. For this we use a simple “dashboard” below that allow us to change the payoffs and observe the equilibrium flow direction so implied. We hope that a full theoretical treatment would yield similar insights, while correcting any misperceptions that result from this rather simplified approach.

Rock Scissors Paper v2

To experiment with this dashboard, download the Rock Scissors Paper cdf file after loading the free Wolfram CDF Reader. Note that the reader does not yet work on smart devices such as iPads.

Negotiation fields: in its simplest form, the game is played based on the idea that for each player, rock breaks (wins over) scissors, scissors cuts (wins over) paper and paper covers (wins over) rock. This is put into game theory format by saying that for each player, they see a unit payoff for each and the negative amount if they lose. If both players play the same thing, the payoff is zero. In game theory, the matrix is called the payoff matrix and appears as the 3-by-3 block matrix in the lower left of the dashboard, one up from the bottom row. The game can be made symmetric by creating the fiction that each person plays both sides: hence the payoff matrix (negative transpose) also appears at the top right, one to the left of the last row. The last row (and last column) represents a “hedge strategy” of the fictional game; it insures that the results of the fictional game exactly match the original payoff. In decision process theory, we take the fictional game as a non-fictional representation of the game with the “hedge” direction re-interpreted as time.

We retain the interpretation of the payoff, which we now call the negotiation field. We make this distinction because the field can change in time and can be thought of as a negotiation between the players. As in game theory, there is a distinct negotiation field matrix for each player, so that the time dependence reflects that player’s internal view of their own preferences and their opponent’s preferences. So for example if you (player p1) believe there is an increase in utility for “rock breaks scissors” from 1 to 2, your ideal strategies change from equal to {0.25, 0.333333, 0.416667} and your opponent (player p2) strategies change from equal to {0.333333, 0.25, 0.416667}. Your opponent should pick up on this preference and play paper more often. You on the other hand are forced to play rock less often because of the competitive nature of game: you play defensively.

Collective Bias Value: game theory makes no strategic distinction between games if their payoffs differ by an overall constant. We call this the collective bias value. You can verify that changing the collective bias value on the dashboard for the baseline case does not change the ideal strategies. The collective bias value for each player reflects a certain way of thinking about decision processes. In most cases, we make decisions assuming the utility of the decision is in our favor. We thus unconsciously add a collective bias value. So for example if you add a value of 0.1 to the payoffs, each payoff for you is positive and each payoff for your competitor is negative. On the dashboard, the collective bias value has been added as a convenient slide, saving you the trouble of moving each of the payoffs up by the same amount.

Valuation fields:  In game theory, when defining the fictional game, when the collective bias has zero (game) value, the last row and the bottom column are zero. This last column (and last row) has values in general proportional to the game value. In decision process theory, we extend this concept. Because we label this column (and corresponding last row) time, the payoffs in this column we distinguish from the negotiation fields and call them the valuation fields. You can use the dashboard to see the ideal strategy in the case that the collective bias value is 0.1 and the valuation fields are 0.1 for player 2 and -0.1 for player 1. The players should have equal and opposite valuation fields because payoffs by their nature are competitive and implicitly zero sum.

We go further however. We see the valuation field for each strategy as generating a force along that strategy, since a player need not value each strategy the same. Set the collective bias value to 0.1, and all the valuations to 0.1. Now change “p2 values rock” from 0.1 to 0.2. This makes no change to your opponent’s (p2) ideal strategies, but does change your (p1) strategies from equal to {0.333333, 0.308333, 0.358333}. This says that you have learned of your opponent’s leaning towards picking rock. It is a bias on your opponent’s part. If you pick paper you will clearly gain an advantage based on your knowledge of your opponent’s bias.

On the other hand, let us say that you (p1) decide to place more valuation on rock and your opponent does not. You change your “p1 values rock” from 0.1 to 0.2. Your ideal strategy does not change this time but your opponent’s does: {0.333333, 0.358333, 0.308333}. It is not symmetric however. The reason is that your valuation of rock moves you towards the origin, toward preferring rock less. This will be compensated by your negotiation forces. This means your opponent can take advantage of your bias by picking paper less, since there is less concern you will pick that. This is compensated by choosing scissors more. Note that in these last two examples, the total rate of making choices is larger for the other player, the player that does not increase their choice.

Inertia: a related attribute of valuation fields and the collective bias value can be seen on the dashboard choice of the “normalized” ideal strategy. The normalization is to pick the time component to be unity. This allows us to make comparisons for different models. Since we argue that increasing the collective bias value should increase the valuation fields, by holding the fields constant we implicitly introduce a new parameter we call the inertia: the ratio of the collective bias value and inertia are thus being held constant. A consequence of this is that the normalized ideal strategy will have “flows” that get smaller as we raise the collective bias value. This substantiates our view that the strategies are the rate of change of preferences in response to the valuation and negotiation forces. A high inertia corresponds to very slow movement.

Internal negotiation fields: A distinct difference between our approach here and game theory is the possibility of capturing internal conflicts, factions and self-payoffs. Suppose our opponent (p2) decides that she is in cyclic conflict over rock and paper in a way which is totally internal. On the dashboard move the slider for this possibility from 0 to 0.2. She has no reason to suppose in this case that we have made any changes in our utilities, so her ideal strategy stays the same. However we may profit from this internal cyclic conflict as seen by our ideal strategy: {0.355556, 0.288889, 0.355556}. We decrease our frequency for scissors to capitalize on the area of conflict.

Ideal strategies and forces: Our approach here has been to identify mechanisms that generate change. We call these forces. So for example, the negotiation field component {i,j} generates a force on our (p1) choices along the “i” direction as a negotiation between our choice and our opponent’s choice along the “j” direction. This is rather different from the valuation force for the component “i” that generates a force along the same direction independent of what our opponent does. When these two types of forces exactly cancel for every strategy, there are no forces moving either our strategies or our opponent’s strategies in either direction, defining an equilibrium position we call the ideal strategy.

Zero-sum games generalized

Posted on by

Arguably, one starting point of game theory is the idea of a zero-sum game. Ordinary games such as chess have a winner and a loser. Games such as poker, exchange money from the losers to the winner. Of course game theory extends the concept of zero-sum games dramatically to situations that are far more general than recreational games. Still, the idea of a zero-sum game separates the class of all games into two distinct camps: those which are essentially competitive and zero-sum and those that have elements of cooperation in which the total value of the game may grow or diminish. In this regard, constant-sum games are considered to be essentially like the zero-sum games except one can imagine that the two sides agree on some tribute that is exchanged, which lies outside the rules of the game.

I argue that decision process theory has much in common with the theory of games so how does a zero-sum game manifest? Or more generally, how does a constant-sum game manifest? In some ways the question is difficult because game theory has a very specific notion of utility, which has been modified in decision process theory. There are several concepts that might play the role of value, from components of the payoff matrix to the concept of preferences that underlie strategy choices. What is clear however about the concept of a zero-sum game is that something must be conserved. There must be some attribute of the decision process that is unchanged; some attribute whose value has no impact on the strategic choices being made. The most appealing approach to me is to associate such a conserved quantity with a collective strategy that is inactive. Such a collective strategy represents a collective preference whose value plays no role in the strategic outcomes. One such collective strategy would be, in some frame of reference, the sum of the strategies of all the players. Interestingly enough, the sum of such strategies in game theory is also a constant.

The concept of a collective strategy being inactive is not quite the same thing however as saying that such a strategy is totally invisible. We have to examine in more detail what is meant by a strategy playing no strategic role. In game theory, this means that the fixed point, the equilibrium point, does not depend on the value of that strategy. In decision process theory, this means that there is a conserved momentum associated with that collective strategy which is conserved. The conservation law is set by the initial conditions. If there is a great deal of initial inertia for example, the decision system will behave quite differently than if there is very little initial inertia. These differences are not seen in game theory: zero sum games are characterized solely by their payoffs, so that two games with the same payoffs should behave identically. I think this makes sense in decision process theory as well when you are at a fixed point. However the behavior around that fixed point should depend on the conserved quantities. Metaphorically, if the system circles the fixed point you should perceive differences depending on the amount of angular momentum the system has, even though that angular momentum is conserved.

How does one identify these conserved quantities? In game theory one identifies games for example in which the payoffs sum to zero or to a constant. These systems are competitive in that what one person wins the other players lose in such a way that exactly compensates the win. Thus competition is one way of identifying situations in which there is a conserved collective strategy. I have argued in decision process theory that a conservation law occurs in societal situations in which there is an established code of conduct to which all players adhere. Let us call such a code of conduct an effective code of conduct. A competitive situation could, by a slight stretch, also be considered an effective code of conduct. All players agree that the rules of the game are that whatever one person gains, the remaining players must provide compensation. I suggest that the conserved quantity must depend in some way on the amount that is exchanged. The more value exchanged, the more risk and hence the more interesting the dynamics required to hold such a process near some equilibrium value. Indeed, this may not be possible and the process may be unstable and fly apart, still maintaining these conservation rules.

I don’t have a strong argument from game theory about what these conserved quantities should be. However from decision process theory, I do have a strong argument: there is a unique quantity identified whenever one has identified an inactive strategy. In physical theories this is the momentum, which in Newtonian theories is the product of the mass and the velocity along that direction. In other words, the inertial mass plays a role as well as the velocity. In more general geometries such as we consider for decision process theory, the momentum still has the same qualitative property. I argue that the momentum is the “value” that we should identify with the game theory notion of a constant-sum game. I go from a direction that provides an effective code of conduct to the identification of a value whose sum is conserved; whose sum is constant independent of any and all dynamic interactions. In this way we have generalized what it means for a process to be zero-sum.

The zero-sum value is really that the sum of the time components of the payoff, the “electric field components,” is zero. This is a direct consequence of the decision effort scale being inactive. Consider a different scenario in which all of the relative player preferences are inactive; only the player efforts are active. In this case, for each player, the time components of the electric fields would be equal. Moreover, we could require that there be no closed loop current flows in the player subspace, which would imply no “magnetic fields” orthogonal to the player subspace. This is the requirement of no self-payoffs or factions. Such a model has much in common with the voting game in game theory.

Thought and inertia

Posted on by

Relative to decision-making, I believe we can distinguish two ways in which the brain generates action. There is reflexive action that takes almost no time. This is the speed of light or thought reaction. There is reflective action that takes significantly more thought and time before action results. The extreme is when time stands still and the action seems to take forever. I use this to introduce the concept of inertia. Inertia is a measure that determines the mixture of these two types of actions. Zero inertia would be the speed of light and infinite inertia would be action that takes forever. The real world stands between these two extremes.

I also introduce the notion of inertial time. This is how time appears to slow down as decisions are made based on thoughtful reflection. Inertial time or reflection provides the possibility of social structures such as codes of conduct. These are strategies that are conserved and appear static or unchanging. Physical time becomes stationary for stationary flow behaviors, though this is not the same as static behavior. In electrical engineering the analogy is a constant current, which allows for the creation of magnetic fields, which for decisions I identify as payoffs. Static charges allow only electric fields and no wave propagation.

What then is inertia? I start with the idea that everything is described by its energy and momenta. It is a geometric structure called a tensor. The characteristics of this structure depend on what it describes. If it is meant to describe something with a property that allows one to see the world from a perspective at rest, then its properties will be characterized by the flow or rate of change to get to that perspective. At rest it will have a rest energy density and by the characteristics we can call stresses that indicate forces to move along specific strategic directions. Technically, these ideas are captured by the statement that the energy momentum is a second order tensor structure that has a time like eigenvector called flow and a positive scalar called the rest energy density.

Though common sense, these concepts are not part of the normal discourse about decision-making. With these concepts we can approach subjects such as entitlement and engagement. For example, we can view an artificial state of a world in which everyone is entitled, which is to say that everyone sees a payoff that is their own creation and is not impacted by decisions made by anyone else. This is possible only if they are totally disengaged from everyone; their own actions and actions by others have no consequences. I say this is an artificial state to the extent that their entitled payoffs lead to no consequences. If there are severe consequences, either positive or negative, then the theory and common sense suggest that a player becomes engaged. As they become engaged, again theory and common sense suggest that their notion of the payoffs will also change. As part of these changes I expect that the energy density will be stronger in some strategic areas than others and hence inertial behaviors will drive what will become the stable collective behaviors of players as they become engaged and whose behavior ceases to be totally entitled.

In many ways this discussion can be carried on without recourse to theory, just to common sense. Where theory comes in is its ability to deal simultaneously with many different mechanisms that are each plausible but mutually interactive. This is as true for this discussion as it is for industrial systems. Our ability to understand deeply is usually limited to essentially linear effects that extend over some small domain. We have difficulty viewing how many mutually interacting linear effects result in non-linear composite behavior. The theory provides the machinery for such visualizations. I have carried out a number of numerical calculations to illustrate this, and a specific example for inertia can be found in The Dynamics of Decision Processes, figure 8-21 to figure 8-24 of section 8.7.1.

Decisions: stochastic or deterministic?

Posted on by

We believe we know the answer to the question of whether decision-making is a stochastic process or a deterministic process. It is clearly not deterministic since we, as human beings, have free choice. It is equally clear that some outcomes are far from surprising; in which case the decisions that led up to those outcomes must have played a decisive role. In physics there are similar situations.

For example if I hope to buy carpet for a room, I first take measurements. In one sense the measurements that I get are random because when I do the measurements multiple times, I usually get multiple answers. In another sense however, we have agreed in our society that the room doesn’t change its dimensions at random and ascribe the multiplicity of measurement answers to measurement error. We take the room dimensions as attributes that exist in the “real world” and our measurement errors as attributes of a flawed process. We make no attempt at making a theory of the flawed process but instead focus on theories that deal with what we perceive to be the real world. We justify our approach in noting that the measurements cluster around some average value with a variance that reflects the accuracy of our measurement tool.

A similar point can be made about decision-making. If we focus on the actual choice made at any one point in time, we may be focusing on a process that has sufficient variability from one person to another that a theory of such processes is not practical. However we may focus instead on the frequency with which a person makes choices from a variety of options. In decision process theory, I argue that these frequencies are part of the physical world with enough regularity that we can profitably construct a theory of their behaviors in time. The real world suggests that such behaviors vary continuously in time as well as along all the dimensions that measure preferences.

Since these assertions are about the world we live in, it should be possible to validate whether decision behaviors from one moment to another occur in a deterministic way. A similar question has been asked about certain biological processes, most notably the behavior of heart beats. Since the biology of the heart is very complex and intimately connected with living organisms as opposed to inert organisms, one might conclude that the heart behavior would be stochastic. This turns out not to be the case and is illustrated by considering “recurrence plots” of the time sequence of heart beats f\left( t \right). One would expect that a contour plot of the heart beats \left| f\left( t \right)-f\left( {{t}'} \right) \right| for different pairs of time would show no structure; one would expect it to look like noise. In fact it shows distinctive structure suggesting that future behaviors of the heart depend on the past behaviors in an organized and continuous fashion.

I propose we look at decision processes in the same way. To illustrate behaviors you might see, I start with a very simple model that displays some of the structures I have seen in numerical evaluation of decision process theory. The simple model emphasizes that the structure I hope to see is not at all esoteric but one that simply has not been noticed much. The important point is that we focus on the behaviors that might follow deterministic rules as opposed to composite behaviors that are mixtures of both deterministic and stochastic effects.

In the simple model I assume two variables, one reflecting time t and the other reflecting some decision preference z. For continuous values of the preference z there is a time sequence, which I take to be given by

g\left( z,t \right)=\cos z\cos t+\sin 2z\sin 3t

There is nothing magic about this choice other than I imagine that in the real world there will typically be multiple frequencies in time and that there will be corresponding variations in preferences. The resultant recurrence plot is provided below as a CDF insert. One can vary the preference and see that the structure will in general depend strongly on the preferences, based on the model.

[WolframCDF source=”http://decisionprocesstheory.com/wp-content/uploads/2012/11/ToyDecisionProcessModel.cdf” width=”805″ height=”723″ altimage=”http://decisionprocesstheory.com/wp-content/uploads/2012/11/ToyDecisionProcessModel.cdf”] CDF Figure: Time sequence recurrence plot for toy model for various preference values starting at  z=0.

I draw attention to two cases. The first is for z=0 in which the single frequency dominates. Seeing periodic behavior in the time behavior of the decision choices would be clear evidence of deterministic behavior. However, it is much simpler than what we would expect from complex structures. The behavior need not be so simple, as can be seen by looking at other values, which display more complex behaviors. To experiment with these behaviors, move the “slider” on the above CDF figure.

This by no means exhausts what we would expect from the real world and by no means exhausts what a realistic theory provides. Decision process theory takes as input time and preference behaviors at some known point. It substantially transforms these inputs into behaviors at all other points of time and preference. Like with physical and geometric theories of this type, the transformations may be essentially linear, in which case the new behaviors look like the old. The transformations may also be non-linear in which case the new behaviors exhibit new phenomena. A simplified process model has been studied extensively by others investigating such new behaviors, as well as looking for complex behaviors, termed creative bios, in physical and biological theories. They have looked for such complex  empirical behaviors in physical and biological processes, such as cosmological behaviors of the early universe and the behaviors of heart beats. Causal behaviors (simple and complex) seem to be more common than commonly believed.

Wolfram Technology Conference 2012

Posted on by

The following is the talk given at the 2012 Wolfram Technology Conference held October 17-19, 2012. The presentation, Wolfram Technology Conference 2012 Talk Final, is a Mathematica slide show and requires the (free) Wolfram CDF Reader. My apologies to those who have not yet installed the reader; currently smart phones do not support this reader so the slides will not be visible on such devices. However, you can open the PDF document directly, or watch the YouTube video.

Download (PDF, 1.85MB)

.

How do we value the future?

Posted on by

I am struck by the difficulty of getting people to value decisions whose worth only comes to fruition in the distant future. I am one of those people, as probably are all of us. In making business decisions, we argue that results must be seen in 12 to 18 months in order for our decisions to be believable. The best decisions are probably those whose impacts are seen immediately or at least in the current quarter. In many ways such  beliefs are solidly based. It is fair to assume that we have all wasted our time on decisions that have yielded no value, or at least much less value than the effort justified. A good friend of mine, H. Kessler, pointed out the following article that addresses some of the issues associated with a common economic approach to valuing the future as it relates to sustainability: http://www.thesolutionsjournal.com/node/1144.

Several things strike me as regards this approach called discounting the future. On the one hand, I think that there is a flaw in thinking about the future in this way, which is also hinted at in the above article. It is true that the net present value of a dollar 20 years from now is less than a dollar today. We use the concept of net present value to compare economic tradeoffs today with costs from the future. As the author points out however, we don’t really know the appropriate discount rate. For sustainability issues, we may be talking about less food or resources in the future based on present actions, which means we are talking about the loss of life in the future. How do we value that loss? The value to be well fed and the value to expect a reasonable life don’t change, even though the dollars assigned might.

On the other hand, I believe decision process theory suggests a different way of approaching the question of value, an approach more along the lines of the Art of War by Sun Tzu. I don’t have the details but my recollection is that the concepts arose out of observing local war lords fighting innumerable small battles. Battles were between villagers and bandits, with much harm and instability resulting for the common people. A mindset change came about by taking a step back and formulating general principles that were adopted by the very people doing the bulk of the fighting.  One such principle was that the best way to fight was not to enter into battle and thus not to fight at all. Such principles I would call components of a code of conduct, an ethical set of rules to be adopted by all, warriors and villagers alike.

I am becoming convinced that solutions for our modern problems that require valuing future costs must be based on a close observation of past behaviors of a similar nature. Like Tzu, we must then identify the new ethical rules that must become part of our Code of Conduct.  The ethical rules must be so well founded that the consequence of not following them should, like in the Art of War, be obvious and immediate. Such rules need to be self validating. This is essential since we all forget from time to time why we adopt even the most obvious ethical behaviors. We must be reminded to do no harm, and to not steal.

Strategic preferences

Posted on by

At the heart of the discussion of strategic decision-making is how to value each agent’s strategic position. In the theory of games, this is based on the notion of utility; the assumption is that each agent values the outcome of the decision independently. I carry over that notion of valuation into decision process theory. I assume that each agent or player can measure the utility of any given strategy by assigning a numerical preference. As in game theory, the player can also measure the utility of a mixture of utilities by thinking of the choice as assigning sequence of frequencies to each pure possibility and making choices with those frequencies over a sequence of plays. In either case the preferences are idiosyncratic: they go with the player who owns those choices.

It is clear that preferences defined in this way provide a numerical position that is more than just a number for each strategy, it represents a physical attribute of the decision-making process. It is very much like a global positioning system for keeping track of positions on the earth; a fair amount of coordination is involved to relate one position to another. We get by with our GPS systems because this complexity is hidden inside our devices. Such a global positioning system is also used in theories of which decision process theory is a special case. My initial approach was to adopt the same strategy as used in such theories to define a positioning system. I have adopted what is called in the literature, harmonic coordinates to define the positions. It requires the definition of a scalar field for each strategic direction. This scalar field captures the physical characteristics of preferences associated with that direction. There are constraints on the behaviors of these scalar fields that arise from the theory that can be verified by detailed analysis of real world behaviors. The theory addresses the detailed coordination alluded to above.

Since many detailed examples are given in the white papers on this site, it may be helpful to put those numerical examples into a more general context. I suggested that a very large class of models, called stationary models in the literature of general relativity, is a useful class of models to study for decision-making. In these models, there is always a frame of reference in which the decision flows are stationary and the distance metric is independent of time. In the formal language of differential geometry, time is an isometry. I specialized to the case in which the flows are not only stationary but zero in this special frame, which I called the central co-moving frame. The detailed coordination described above however is absent in this frame.

To get an idea of why, consider an analog of a wave traveling in water. The coordination of interest is the behavior of the wave. In particular, if one generates a wave at a source, we want to know the behavior of all the subsequent ripples. There is nothing however that prevents us from viewing the wave from the perspective of an army of corks uniformly distributed and riding on the surface of the water. Each cork, from his point of view, is at rest (co-moving). The model assumption is that over time, the attributes of the water are constant for each cork (though in principle different for different corks). The cork doesn’t see anything of direct interest to us. Nevertheless, from the behavior of each cork, we gain spatial knowledge about the water. That knowledge can be used to reconstruct the ripple behavior if we add additional equations. The harmonic equations from differential geometry are just such additional equations. They take the spatial information from the co-moving frame and provide wave equations that depend on that spatial information to project the behavior of the ripples that might occur.

Software delivery schedules and standing waves

Posted on by

I worked on a large software development project in which the most interesting thing was why the project was delivered two years late to the customer. Both the customer and we, the vendor, knew from the outset what was required for the project. We both agreed on the work that needed to be accomplished and the time it would take to accomplish that work. About half way through the completion of the project, the customer added new requirements, which we as the vendor agreed could be done maintaining the original schedule, but with a known amount of increased effort.

We both looked at the project from a static perspective: we based our estimate of the initial effort on jobs we had done in the past that were similar. We estimated the increased efforts due to additional requirements on the same historical data. This view looks at the completion date as a random event distributed with a normal distribution having a small error. The shape of the distribution, including the standard deviation, is based on the historical data. Despite the best efforts of the development team, the total effort needed to complete the project as well as the delivery time were vastly underestimated.

I believe that the lessons learned from this project are directly related to the need to view the software delivery process as a dynamic as opposed to a static process. We in fact brought in an outside (Systems Dynamics) consultant on the project and learned the following.

  • Our detailed understanding of the project was fundamentally correct: the number of engineers needed to produce a given amount of code didn’t change after the new requirements were added.
  • Our understanding of the quality of the code produced by the engineers didn’t change based on an assessment of their skill set.
  • It was well understood that new hires would be less skilled than those with training in the areas under development. Despite this understanding, standard practice was to not take into account such details when doing cost and schedule estimates. Normally, such differences would generate small increases in costs associated with training.

Though there were many other factors, these three lessons were already sufficient to gain an understanding of why the costs and schedules were terribly out of whack. Let’s say that skilled developers would develop code that contained at most 10% errors. For argument sake, suppose that the delivery of product to the customer would allow 1% error. Suppose further that a test cycle to determine errors would take 6 months and that this was built into the original schedule. One test cycle after initial completion is sufficient to deliver a product of the requisite quality. Now imagine the situation of adding new requirements with the commensurate hiring of new personnel with less experience on the product. Because of the new hires, the initial delivery would contain many more errors, say as an example, 25% errors. So if we start with 100 units, we have 25 units that have errors after the initial pass. After the planned 6 months, we have 25/4 units with errors assuming the same quality of testing and fixing, which is not sufficient to deliver a quality product. This means an additional 6 months of testing, which gets us down to 25/16. To get below the 1 defect requirement, we now need an additional 6 months of testing, to reach the defect level of 25/64. Thus we get an additional year of development because of the change in quality of the new hires.

The actual quality was worse on the project and there were a few other factors, but the essential aspect of the story is unchanged: a dynamic look at the mechanisms demonstrates that small factors lead to unexpected and huge effects. This example illustrates how decisions propagate and impact outcomes. Decision process theory provides a theoretical foundation for such effects that is illustrated in the various models that we have detailed in our white papers. In this software example, we were misled when we assumed certain effects were static, such as the quality of the engineers. We assumed that the engineers would instantly become experts, ignoring what we equally well knew to be true that a training period was needed to make that happen; such a training period could in fact be a couple of years, well beyond the time we allowed for a development cycle.

There are examples in physics where we also make such assumptions, which don’t usually cause problems, but again can lead to incorrect results. A mechanism that is closely related to decision process theory would be that of gravity. In physics we assume that for most purposes, gravity is static. Under extreme conditions however, this is a bad assumption. If our sun were to explode, we would not feel the gravitational effect for several minutes because of the time it takes for the cause to make its effect felt. Such effects might be labeled gravity waves, despite our incorrectly labeling of gravity as a static scalar field.

In decision process theory, it is also true that causes generate effects that are separated by a finite time. There is always a propagation speed: effects are never instantaneous. In our models, in our model calculations we have focused initially on streamlines, which are paths along which the scalar fields are constants. For a picture, imagine the motion of air with smoke; the smoke provides visual evidence of the behavior of the streamline. One specific model might be of someone speaking, whose voice generates sound waves. We would capture the streamlines as displaying a global wave pattern, one that is not visible on any one streamline. Once sound waves are generated, we would see the streamlines undulate: the path of a velocity peak would propagate with a form we call a harmonic standing wave, analogous to shaking a jump rope whose other end is attached to a wall. This wave velocity is quite distinct from, and often much faster than, the media velocity.

Here is a model calculation using Mathematica of what a harmonic standing wave looks like in decision process theory for an attack-defense model:

[WolframCDF source=”http://decisionprocesstheory.com/wp-content/uploads/2012/08/network-waves-pressure-plot.cdf” width=”328″ height=”317″ altimage=”http://decisionprocesstheory.com/wp-content/uploads/2012/08/network-waves-pressure-plot.cdf”]

The myth of a level playing field

Posted on by

I unconsciously subscribe to the view that each day starts anew with new possibilities; I start fresh with no residue from the past. I call this a level playing field. Whatever happened yesterday is of no consequence to today. Decisions that were made yesterday have no ripple into today. This does not agree with reality and is a new feature captured in the theoretical treatment I give to decisions, see Geometry, Language and Strategy, Thomas, 2006, World Scientific (New York).  Some actions carry through while others die out. There are consequences to our actions that sometimes extend into days, weeks or years.

So why do I subscribe to this short-term view knowing full well that there are significant exceptions? I think it is related to similar ideas in mathematics and physics that it is easier to visualize events as local occurrences. For example, we see the earth as flat and stationary. That is our local frame of reference. The earth’s curvature is not easy to grasp. The effects of its rotation about its axis and around the sun are equally hard to grasp.

We make a similar simplification in business when we focus too closely on local effects. We totally understand the consequences of hiring an experienced person versus an inexperienced person in terms of their quality of work. It is less clear how such differences are expected to show up in terms of project schedules.  It is hard to see how such simple mechanisms work together to create system behaviors. In this case as in physics, it is easy to grasp local effects but hard to grasp global effects.

The idea of a level playing field is analogous to the idea that the earth is flat. This assumption is often useful  even though it may ignore important (global) effects that are not important unless you look at large “behavioral distances” or long “behavioral times”. For example if you deny a portion of the population education, adequate nourishment and shelter, this may contribute to the greatest good for the greatest number of people. We say such behavior is not just either because of our ethical position or because logically, we understand that over a long period of time, you have created an unstable society, one that may reverse the roles of the populations.

The problem in economics and in society is that our current theories are local, not global. They highlight the obvious advantages of a flat earth but fail to take into account its curvature when looking beyond the local. it is hard to translate these differences into our expectations of what should happen. And yet we know that a long-term view is essential to understanding. I conclude that however useful, the concept of a level playing field is a myth.

I have argued for the importance of considering both short-term cycles and long-term cycles. That concept I think is particularly helpful in moving beyond the myth of a level playing field. We can still wake up each day and start fresh as long as we understand that we are missing some of the long-term cycle effects. We must be prepared to predict the consequences of the composite behaviors: there will be some situations in which one or the other dominates, and other situations where both are comparable.

I believe that the goal of a theory in physics or in society should be to help provide a mechanism for discussion. The theory must be able to take into account all relevant and significant mechanisms. I argue here that one of those mechanisms is the degree to which the field is not level.

Sustainability–short and long cycles

Posted on by

In many discussions of sustainability, the assumption is made that the distant past and the distant future have no direct relevance to the immediate present. This assumption is not unreasonable since ripples from the past often do die out by the time they reach the present; similarly events in the present generate ripples that often die out if we wait a sufficiently long time. There must be some basis for our belief that events can be considered unconnected. We capture that belief in the use of probability as a means to predict the future: Bayesian probability.

I argue that this assumption is incorrect. See Geometry, Language and Strategy, Thomas, 2006, World Scientific (New York).  There are longterm cyclic effects that originate in the past, whose effects don’t die out. Some events from the present will continue on into the future without appreciable damping. The justification for this argument is as common sense as the above assumption. We see boom and bust cycles in market behaviors; we see the longterm consequences of global wars. The appeal of the above assumption is its simplicity, not its accuracy. I argue that if we had a theory that took into account such longterm cycles, we would consider that theory superior. We would see choices fluctuate according to both the short-term and long-term cycles (e.g. the following CDF figure based on an attack-defense model, chapter 9 of the dynamics of decision processes illustrates choice behavior with two cycles; the CDF format is not yet supported on smart phones, sorry).

[WolframCDF source=”http://decisionprocesstheory.com/wp-content/uploads/2012/08/Two-cycle-strategies.cdf” width=”328″ height=”334″ altimage=”http://decisionprocesstheory.com/wp-content/uploads/2012/08/Two-cycle-strategies.cdf”]

An attribute we would look for in a more complete explanation of events would be that longterm cycles, though hard to see (weakly coupled to our observations), can have very strong effects (payoffs). This would contrast with our experiences of the day-to-day short cycle time events that are easy to see (strongly coupled to our observations), but with relatively weak effects (payoffs).

How would this view change our understanding of sustainability? We might then understand that as human beings we make small changes (weak coupling) to our environment that over a long time cycle time can have strong effects (payoffs). Because we have been successful in the past to accommodate environmental changes is no guarantee that we will be as successful in the future.